已知复数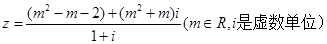 是纯虚数。
是纯虚数。
(1)求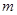 的值;
的值;
(2)若复数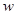 ,满足
,满足 ,求
,求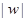 的最大值。
的最大值。
二阶矩阵M对应的变换将点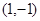 与
与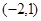 分别变换成点
分别变换成点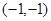 与
与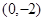 .
.
(Ⅰ)求矩阵M的逆矩阵 ;
;
(Ⅱ)设直线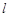 在变换M作用下得到了直线
在变换M作用下得到了直线 :
: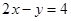 ,求直线
,求直线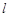 的方程.
的方程.
已知数列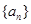 的各项都是正数,且满足:
的各项都是正数,且满足:
(1)求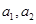 ;
;
(2)证明: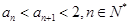
是否存在实数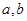 使得关于n的等式
使得关于n的等式
成立?若存在,求出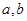 的值并证明等式,若不存在,请说明理由.
的值并证明等式,若不存在,请说明理由.
有4男3女共7位同学从前到后排成一列.
(1)有多少种不同方法?
(2)甲不站在排头,有多少种不同方法?
(3)三名女生互不相邻,有多少种不同方法?
(4)3名女生在队伍中按从前到后从高到矮顺序排列,有多少种不同方法?
(5)3名女生必须站在一起,有多少种不同方法?