中午,一根1.5米长的木杆影长1.0米,一座高21米的住宅楼的影子是否会落在相距米远的商业楼上?傍晚,该木杆的影子长为2.0米,这时住宅楼的影子是否会落在商业楼上?为什么?
班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生的发言次数进行了统计,并绘制成如图1的频数分布折线图.
(1)请根据图1,回答下列问题:
①这个班共有______名学生,发言次数是5次的男生有____人、女生有____人;
②男、女生发言次数的中位数分别是____ 次和______次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2.求第二天发言次数增加3次的学生人数和全班增加的发言总次数.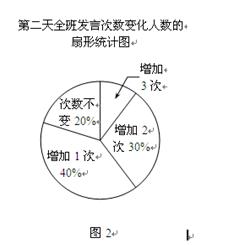
已知一元二次方程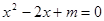 .
.
(1)若方程有两个实数根,求m的范围;
(2)若方程的两个实数根为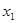 ,
,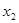 ,且
,且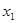 +3
+3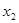 =3,求m的值。
=3,求m的值。
先化简: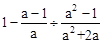 ,再选取一个合适的a值代入计算.
,再选取一个合适的a值代入计算.
(1)计算: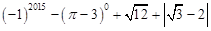
(2)化简:
如图,在平面直角坐标系中,抛物线y=﹣ x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.
x2+bx+c与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.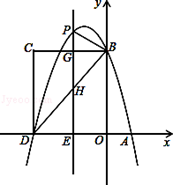
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.