．(
本小题满分13分)
某慈善机构举办一次募捐演出，有一万人参加，每人一张门票，每张100元. 在演出过程中穿插抽奖活动．第一轮抽奖从这一万张票根中随机抽取10张，其持有者获得价值1000元的奖品，并参加第二轮抽奖活动．第二轮抽奖由第一轮获奖者独立操作按钮，电脑随机产生两个数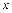
，
（，
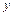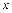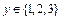），随即按如右所示程序框图运行相应程序．若电脑显示“中奖”，则抽奖者获得9000元奖金；若电脑显示“谢谢”，则不中奖．
（Ⅰ）已知小曹在第一轮抽奖中被抽中，
求小曹在第二轮抽奖中获奖的概率；
（Ⅱ）若小叶参加了此次活动，求小叶参加此次活动收益的期望；
（Ⅲ）若此次募捐除奖品和奖金外，不计其它支出，该机构想获得96万元的慈善款．问该慈善机构此次募捐
是否能达到预期目标．
。
时，
的最小值为－1，求实数k的值；
，均存在以
为三边边长的三角形，求实数k的取值范围。
的图象在点
处的切线方程为
。
的解析式；
在区间
上恰有两个相异实根，求m的取值范围。
中，角A,B,C所对的边分别是
，且
。
，求周长
的最大值。
，且
。
时，且
，求x的值；
，求
的单调递增区间。
，且
。求
的值。