一个袋中有10个大小相同的黑球、白球和红球,已知从袋中任意摸出一个球,得到黑球的概率是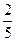 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是
(1)求袋中白球的个数;
(2)若将其中的红球拿出,从剩余的球中一次摸出3个球,求恰好摸到2个白球的概率;
(3)在(2)的条件下,一次摸出3个球,求取得白球数X的数学期望。
扇形AOB的周长为8 cm.
(1)若这个扇形的面积为3 cm2,求圆心角的大小;
(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB.
已知角α终边经过点P(x,-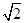 )(x≠0),且cosα=
)(x≠0),且cosα=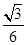 x,求sinα、tanα的值.
x,求sinα、tanα的值.
已知扇形OAB的圆心角α为120°,半径长为6,
(1)求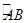 的弧长;
的弧长;
(2)求弓形OAB的面积.
已知角θ的终边上有一点P(x,-1)(x≠0),且tanθ=-x,求sinθ,cosθ.
某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB′交DC于点P.当△ADP的面积最大时最节能,凹多边形ACB′PD的面积最大时制冷效果最好.
(1)设AB=x(米),用x表示图中DP的长度,并写出x的取值范围;
(2)若要求最节能,应怎样设计薄板的长和宽?
(3)若要求制冷效果最好,应怎样设计薄板的长和宽?