如图，
ABC和DBC所在的平面互相垂直，且AB=BC=BD，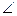
CBA=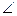DBC= 60°，(1) 求证：直线AD⊥直线BC；(2)求直线AD与平面BCD所成角的大小。
（本小题共13分）已知椭圆
的右焦点为
，
为椭圆的上顶点，
为坐标原点，且△
是等腰直角三角形．
（Ⅰ）求椭圆的方程；
（Ⅱ）过点分别作直线
，
交椭圆于
，
两点，设两直线的斜率分别为
，
，且
，证明：直线
过定点（
）．
（本小题共13分）已知函数
.
（Ⅰ）若
，求曲线
在点
处的切线方程；
（Ⅱ）若函数
在区间
上单调递增，求实数
的取值范围．
（本小题共14分）如图，在四棱锥
中，底面
是正方形，
平面， 
是
中点，
为线段
上一点.
（Ⅰ）求证：
；
（Ⅱ）试确定点在线段上的位置，使
//平面
，并说明理由.
（本小题共13分）在等差数列
中，
，其前
项和为
，等比数列
的各项均为正数，
，公比为
，且
， 
．
（Ⅰ）求
与
；
（Ⅱ）数列
满足
，求
的前项和
．
（本小题共13分）已知△
中，角
，
，
的对边分别为
，
，
，且
，
．
（Ⅰ）若
，求
；
（Ⅱ）若
，求．