（本小题满分12分）
某校高三一次月考之后，为了了解数学学科的学习情况，现从中随机抽出若干名学生此次的数学成绩，按成绩分组，制成右面频率分布表： 
（1）若每组数据用该组区间的中点值（例如区间[90，100）的中点值是95）作为代表，试估计该校高三学生本次月考的平均分；
（2）如果把表中的频率近似地看作每个学生在这次考试中取得相应成绩的概率，那么从所有学生中采用逐个抽取的方法任意抽取3名学生的成绩，并记成绩落在[110，130）中的学生数为ξ，求：
①在三次抽取过程
中至少有两次连续抽中成绩在[110，130）
中的概率；
②ξ的分布列和数学期望．（注：本小题结果可用分数表示）
(本小题满分12分)
已知函数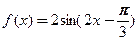
．
（1）求
的单调递增区间；
（2）求的最大值及取得最大值时相应的
的值．
(本小题满分10分)
已知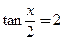
．
（1）求
的值；
（2）求
的值．
在数列｛an｝中，a1=2，a4=8，且满足an+2=2an+1－an（n∈N*）
（1）求数列｛an｝的通项公式
（2）设bn=2n-1·an，求数列｛bn｝的前n项和sn
围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（旧墙需维修），其他三面围墙需新建，在旧墙对面的新墙上要留一个宽度为2m的进出口如图所示。已知旧墙的维修费用为45元/m，新墙的造价为180元/m。设利用旧墙的长度为x（单位：m），修建此矩形场地的总费用为y（单位：元）
（1）将y表示为x的函数
（2）试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用
解关于x的不等式ax2－(a＋1)x＋1＜0．