（本小题满分12分）
已知椭圆E：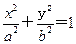
（a>b>0）的离心率e＝
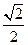，左、右焦点分别为F1、F2，点P（2,
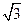），点F2在线段PF1的中垂线上
（1）求椭圆E的方程；
（2）设l1，l2是过点G（
，0）且互相垂直的两条直线，l1交E于A，
B两点，l2交E于C，D两点，求l1的斜率k的取值范围；
（3）在（2）的条件下，设AB，CD的中点分别为M，N，试问直线MN是否恒过定点?
若经过
，求出该定点坐标；若不经过，请说明理由。
某森林出现火灾，火势正以100m2/分钟的速度顺风蔓延，消防站接到报警立即派消防队员前去，在火灾发生后5分钟到达救火现场，已知消防队员在现场平均每人灭火50m2/分钟，所消耗的灭火材料，劳务津贴等费用为人均125元/分钟，另附加每次救火所耗损的车辆、器械和装备等费用人均100元，而烧毁森林的损失费60元/m2，应该派多少消防队员前去救火才能使总损失最少？
已知函数f(x)＝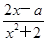
在区间[－1，1]上是增函数．
(1)求实数a的值组成的集合A；
(2)设x1、x2是关于x的方程f(x)＝
的两个相异实根，若对任意a∈A及t∈[－1，1]，不等式m2＋tm＋1≥|x1－x2|恒成立，求实数m的取值范围．
不等式(－1)na<2＋
对任意n∈N*恒成立，求实数a的取值范围．
若不等式组
的解集中所含整数解只有－2，求k的取值范围．
某造纸厂拟建一座平面图形为矩形且面积为162m2的三级污水处理池，池的深度一定(平面图如图所示)，如果池四周围墙建造单价为400元/m2，中间两道隔墙建造单价为248元/m2，池底建造单价为80元/m2，水池所有墙的厚度忽略不计．
(1)试设计污水处理池的长和宽，使总造价最低，并求出最低总造价；
(2)若由于地形限制，该池的长和宽都不能超过16m，试设计污水池的长和宽，使总造价最低，并求出最低总造价．