(本小题满分12分)
有一块边长为4的正方形钢板,现对其切割、焊接成一个长方体无盖容器(切、焊损耗忽略不计).有人应用数学知识作如下设计:在钢板的四个角处各切去一个小正方形,剩余部分围成一个长方体,该长方体的高是小正方形的边长.
(1)请你求出这种切割、焊接而成的长方体容器的最大容积V1; (2)请你判断上述方案是否是最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积V2>V1.
(2)请你判断上述方案是否是最佳方案,若不是,请设计一种新方案,使材料浪费最少,且所得长方体容器的容积V2>V1.
如图,在四棱锥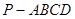 中,
中,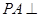 底面
底面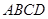 ,
,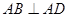 ,点E在线段AD上,且CE//AB。
,点E在线段AD上,且CE//AB。
(1)求证:CE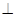 PAD;
PAD;
(2)若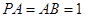 ,AD=3,CD=
,AD=3,CD=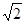 ,
,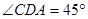 ,求四棱锥
,求四棱锥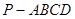 的体积。
的体积。
已知 为坐标原点,
为坐标原点,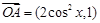 ,
,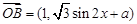 (
(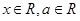 ,
,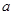 是常数),若
是常数),若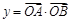 .
.
(1)求 关于
关于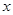 的函数关系式
的函数关系式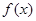 ;
;
(2)若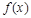 的最大值为
的最大值为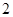 ,求
,求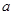 的值;
的值;
(3)利用(2)的结论,用“五点法”作出函数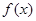 在长度为一个周期的闭区间上的简图,并指出函数
在长度为一个周期的闭区间上的简图,并指出函数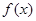 的单调区间
的单调区间
若函数f(x)=sin2ax- sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为
sinaxcosax(a>0)的图象与直线y=m相切,相邻切点之间的距离为 .
.
(1)求m和a的值;
(2)若点A(x0,y0)是y=f(x)图象的对称中心,且x0∈ ,求点A的坐标.
,求点A的坐标.
若a,b是两个不共线的非零向量,t∈R.
(1)若a,b起点相同,t为何值时,a,tb,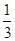 (a+b)三向量的终点在一直线上?
(a+b)三向量的终点在一直线上?
(2)若|a|=|b|且a与b夹角为60°,t为何值时,|a-tb|的值最小?
已知函数f (x)=(1+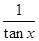 )sin2x-2sin(x+
)sin2x-2sin(x+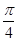 )sin(x-
)sin(x-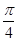 ).
).
(1)若tanα=2,求f(α);
(2)若x∈[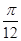 ,
, ],求f(x)的取值范围
],求f(x)的取值范围