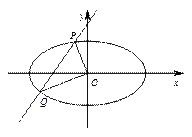
用符号语言表示下列语句,并画出图形.
三个平面α、β、γ交于一点P, 且平面α与平面β 交于PA, 平面α与平面γ交于PB,平面β与平面γ交于PC
交于PA, 平面α与平面γ交于PB,平面β与平面γ交于PC
如图,已知高为3的棱柱ABC-A1B1C1的底面是边长为1的正三角形,求三棱锥B1-ABC的体积。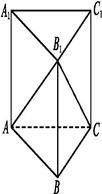
已知圆台的上、下底面半径分别是2 ,5 , 且侧面积等于两底面面积之和,求该圆台的母线长。
如图,在平面直角坐标系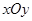 中,
中, 、
、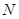 分别是椭圆
分别是椭圆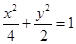 的顶点,过坐标原点的直线交椭圆于
的顶点,过坐标原点的直线交椭圆于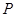 、
、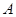 两点,其中
两点,其中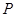 在第一象限.过
在第一象限.过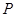 作
作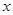 轴的垂线,垂足为
轴的垂线,垂足为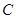 .连接
.连接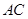 ,并延长交椭圆于点
,并延长交椭圆于点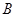 .设直线
.设直线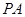 的斜率为
的斜率为 .
.
(Ⅰ)当直线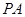 平分线段
平分线段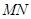 时,求
时,求 的值;
的值;
(Ⅱ)当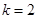 时,求点
时,求点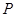 到直线
到直线 的距离;
的距离;
(Ⅲ)对任意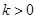 ,求证:
,求证: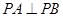 .
.
(12分) 在直角坐标系 中,点
中,点 到点
到点 ,
,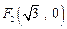 的距离之和是
的距离之和是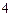 ,点
,点 的轨迹是
的轨迹是 ,直线
,直线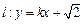 与轨迹
与轨迹 交于不同的两点
交于不同的两点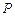 和
和 .⑴求轨迹
.⑴求轨迹 的方程;⑵是否存在常数
的方程;⑵是否存在常数 ,
,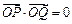 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.