(本小题满分12分)
如图,已知在坐标平面xOy内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△ PMN的面积为
PMN的面积为 ,点A的坐标为(1+
,点A的坐标为(1+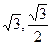 ),
), 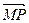 =m·
=m·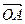 (m为常数),
(m为常数),
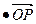


(1)求以M、N为焦点且过点P的椭圆方程;
(2)过点B(-1,0)的直线l交椭圆于C、D两点,交直线x=-4于点E,点B、E分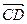 的比分别为λ1、λ2,求λ1+λ2的值。
的比分别为λ1、λ2,求λ1+λ2的值。
已知点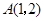 ,在坐标轴上求一点
,在坐标轴上求一点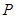 ,使直线
,使直线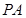 的倾斜角为
的倾斜角为 .
.
如图所示,正方体ABCD—A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F,且B1E=C1F.求证:EF∥平面ABCD.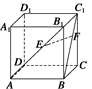
已知正△ABC的边长为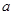 , CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
, CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.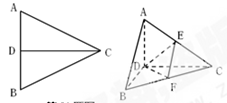
(1)试判断折叠后直线AB与平面DEF的位置关系,并说明理由;
(2)若棱锥E-DFC的体积为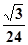 ,求
,求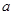 的值;
的值;
(3)在线段AC上是否存在一点P,使BP⊥DF?如果存在,求出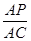 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
已知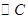 与两平行直线
与两平行直线 都相切,且圆心
都相切,且圆心 在直线
在直线 上,
上,
(Ⅰ)求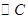 的方程;
的方程;
(Ⅱ)斜率为2的直线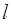 与
与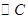 相交于
相交于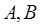 两点,
两点,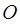 为坐标原点且满足
为坐标原点且满足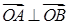 ,求直线
,求直线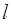 的方程。
的方程。
【原创】如图,在正方体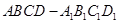 中
中
①求证: 平面
平面 ;
;
②求证: 与平面
与平面 的交点
的交点 是
是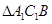 的中心(正三角形五心合一,统称中心)
的中心(正三角形五心合一,统称中心)