本题(1)(2)(3)三个选答题,每小题5分,请考生任选1题作答,如果多做,则按所做的前1题计分.
(1)(选修4-1,几何证明选讲)如图,在直角梯形ABCD中,DC∥AB, CB⊥AB,AB=AD=
CB⊥AB,AB=AD= a,CD=
a,CD=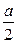 ,点E,F分别为线段AB,CD的中点,则EF=" " .
,点E,F分别为线段AB,CD的中点,则EF=" " .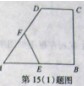
(2)(选修4-4,坐标系与参数方程)在极坐标系(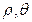 )
)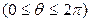 中,曲线
中,曲线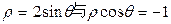 的交点的极坐标为 .
的交点的极坐标为 .
(3)(选修4-1,不等式选讲)
已知函数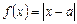 .若不等式
.若不等式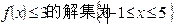 ,则实数
,则实数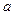 的值为 .
的值为 .
若函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是单调增函数,如果实数t满足f(t)+f(﹣t)<2f(1),那么t的取值范围是_________ .
已知点P(x,y)的坐标满足 ,则z=x+2y的最大值为_________ .
,则z=x+2y的最大值为_________ .
设△ABC的内角A,B,C的对边分别为a,b,c,且a=1,b=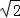 ,cosC=﹣
,cosC=﹣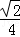 ,则sinB= _________ .
,则sinB= _________ .
若曲线y=ax+lnx在点(1,a)处的切线方程为y=2x+b,则b= _________ .
将a,b都是整数的点(a,b)称为整点,若在圆x2+y2﹣6x+5=0内的整点中任取一点M,则点M到直线2x+y﹣12=0的距离大于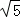 的概率为_________ .
的概率为_________ .