已知矩阵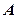 =
=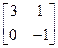 ,求
,求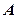 的特征值
的特征值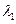 ,
,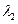 及对应的特征向量
及对应的特征向量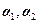 .
.
(本小题共13分)长时间用手机上网严重影响着学生的身体健康,某校为了解A,B两班学生手机上网的时长,分别从这两个班中随机抽取5名同学进行调查,将他们平均每周手机上网的时长作为样本,绘制成茎叶图如图所示(图中的茎表示十位数字,叶表示个位数字).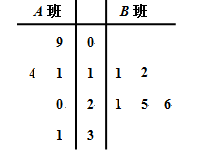
(Ⅰ)分别求出图中所给两组样本数据的平均值,并据此估计,哪个班的学生平均上网时间较长;
(Ⅱ)从A班的样本数据中随机抽取一个不超过21的数据记为a,从B班的样本数据中随机抽取一个不超过21的数据记为b,求a>b的概率.
(本小题共13分)已知等差数列 的前
的前 项和为
项和为 ,等比数列
,等比数列 满足
满足 ,
,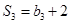 ,
,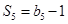 .
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)如果数列 为递增数列,求数列
为递增数列,求数列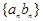 的前
的前 项和
项和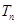 .
.
(本小题共13分)已知函数 (其中
(其中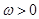 ,
,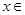 R)的最小正周期为
R)的最小正周期为 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)如果 ,且
,且 ,求
,求 的值.
的值.
已知函数
(Ⅰ)当 时,求使
时,求使 成立的
成立的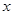 的值;
的值;
(Ⅱ)当 ,求函数
,求函数 在
在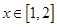 上的最大值;
上的最大值;
(Ⅲ)对于给定的正数 ,有一个最大的正数
,有一个最大的正数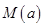 ,使
,使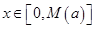 时,都有
时,都有 ,试求出这个正数
,试求出这个正数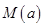 ,并求它的取值范围.
,并求它的取值范围.
已知二次函数 满足
满足 ,且关于
,且关于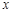 的方程
的方程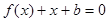 的两个实数根分别在区间
的两个实数根分别在区间 、
、 内.
内.
(1)求实数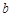 的取值范围;
的取值范围;
(2)若函数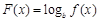 在区间
在区间 上具有单调性,求实数
上具有单调性,求实数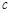 的取值范围.
的取值范围.