( 本题满分12分)已知 为
为 的外心,以线段
的外心,以线段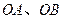 为邻边作平行四边形,第四个顶点为
为邻边作平行四边形,第四个顶点为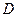 ,再以
,再以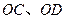 为邻边作平行四边形,它的第四个顶点为
为邻边作平行四边形,它的第四个顶点为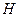 .
.
(1) 若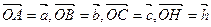 ,试用
,试用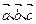 表示
表示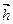 ; (2)证明:
; (2)证明: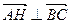 ;
;
(3)若 的
的 外接圆的半径为
外接圆的半径为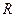 ,用
,用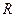 表示
表示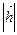 .
.
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.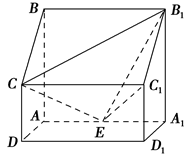
(1)证明B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ,求线段AM的长.
,求线段AM的长.
在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,且PA⊥平面ABCD.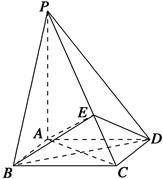
(1)求证:PC⊥BD;
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值.
①求此时四棱锥E-ABCD的高;
②求二面角A-DE-B的正弦值的大小.
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角CPBA的余弦值.
如图,在四棱台ABCD-A1B1C1D1中,D1D⊥平面ABCD,底面ABCD是平行四边形,AB=2AD,AD=A1B1,∠BAD=60°.
(1)证明:AA1⊥BD;
(2)证明:CC1∥平面A1BD.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,M是PD的中点,AB=2,∠BAD=60°.
(1)求证:OM∥平面PAB;
(2)求证:平面PBD⊥平面PAC;
(3)当四棱锥P-ABCD的体积等于 时,求PB的长.
时,求PB的长.