((本题16分)
(1)用红、黄、蓝、白四种不同颜色的鲜花布置如图一所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域用不同颜色鲜花,问共有多少种不同的摆放方案?
(2)用红、黄、蓝、白、橙五种不同颜色的鲜花布置如图二所示的花圃,要求同一区域上用同一种颜色鲜花,相邻区域使用不同颜色鲜花.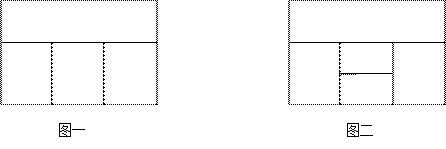
①求恰有两个区域用红色鲜花的概率;
②记花圃中红色鲜花区域的块数为S,求它的分布列及其数学期望E(S).
已知点 为圆周
为圆周 的动点,过
的动点,过 点作
点作 轴,垂足为
轴,垂足为 ,设线段
,设线段 的中点为
的中点为 ,记点
,记点 的轨迹方程为
的轨迹方程为 ,点
,点
(1)求动点 的轨迹方程
的轨迹方程 ;
;
(2)若斜率为 的另一个交点为
的另一个交点为 ,求
,求 面积的最大值及此时直线
面积的最大值及此时直线 的方程;
的方程;
(3)是否存在方向向量 的直线
的直线 交与两个不同的点
交与两个不同的点 ,且有
,且有 ?若存在,求出
?若存在,求出 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
已知 与曲线
与曲线 在点(1,0)处相切,
在点(1,0)处相切, 为该曲线另一条切线,且
为该曲线另一条切线,且 .
.
(1)求直线 及直线
及直线 的方程;
的方程;
(2)求由直线 和x轴所围成的三角形的面积.
和x轴所围成的三角形的面积.
已知椭圆 的焦点为
的焦点为 ,抛物线
,抛物线 与椭圆在第一象限的交点为
与椭圆在第一象限的交点为 ,若
,若 。
。
(1)求 的面积;
的面积;
(2)求此抛物线的方程。
在平面直角坐标系 中,点P到两点
中,点P到两点 ,
,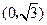 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为 .
.
(1)写出 的方程;
的方程;
(2)设直线 与
与 交于
交于 两点,
两点, 为何值时
为何值时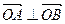 ?
?
已知圆心为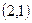 的圆
的圆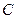 与直线
与直线 相切。
相切。
(1)求圆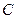 的标准方程;
的标准方程;
(2)若圆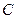 与圆
与圆 相交于
相交于 两点,求直线
两点,求直线 的方程。(用一般式表示)
的方程。(用一般式表示)