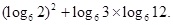（本小题满分12分）
如图，四棱锥
的底面
为菱形，
平面，
，
分别为
的中点，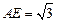
．
（Ⅰ）求证：平面
平面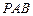
．
（Ⅱ）求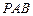平面与平面
所成的锐二面角的余弦值．
设函数
是奇函数．
（Ⅰ）求常数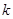
的值；
（Ⅱ）若
，
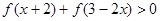，求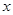
的取值范围；
（Ⅲ）若
，且函数
在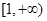
上的最小值为
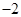，求
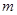的值．
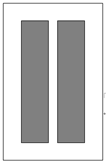
如图，要设计一张矩形广告牌，该广告牌含有大小相等的左右两个矩形栏目（即图中阴影部分），这两栏的面积之和为18000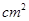
,四周空白的宽度为10
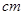，两栏之间的中缝空白的宽度为5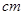，设广告牌的高为
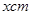，宽为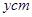
（Ⅰ）试用
表示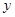
；
（Ⅱ）用表示广告牌的面积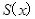
；
（Ⅲ）广告牌的高取多少时，可使广告牌的面积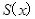最小？
已知f（x）是二次函数，不等式f（x）＜0的解集是（0,5），且f（x）在区间[－1,4]上的最大值是12．
（Ⅰ）求f（x）的解析式；
（Ⅱ）求f（x）在区间
上的最小值．
已知函数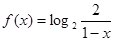
．
（Ⅰ）求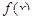
的定义域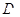
及其零点；
（Ⅱ）判断函数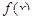在定义域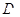上的单调性，并用函数单调性定义证明．
（Ⅰ）求值：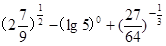
（Ⅱ）求值：