(本小题满分10分)选修4-4:坐标系与参数方程
如图,已知点 ,
,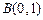 ,圆
,圆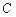 是以
是以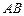 为直径的圆,直线
为直径的圆,直线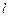 :
: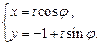
( 为参数).
为参数).
(Ⅰ)写出圆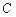 的普通方程并选取适当的参数改写为参数方程;
的普通方程并选取适当的参数改写为参数方程;
(Ⅱ)过原点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,若动点
,若动点 满足
满足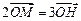 ,当
,当 变化时,求点
变化时,求点 轨迹的参数方程,并指出它是什么曲线.
轨迹的参数方程,并指出它是什么曲线.
(本小题满分12分)根据我国发布了新修订的《环境空气质量标准》指出空气质量指数在 为优秀,人类可正常活动.某市环保局对该市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为
为优秀,人类可正常活动.某市环保局对该市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 ,
,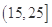 ,
, 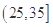 ,
, 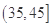 ,由此得到样本的空气质量指数频率分布直方图.
,由此得到样本的空气质量指数频率分布直方图.
(Ⅰ)若空气质量指数大于或等于15且小于35认为是良好的,求该市在这次监测中空气质量
为良好的天数,并根据频率分布直方图估计这一年度的空气质量指数的平均值;
(Ⅱ)如果空气质量指数不超过15,就认定空气质量为“优”,则从这一年的监测数据中随机
抽取3天的数值,其中达到“优”的天数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)如图1,在 中,
中, ,
, 分别是
分别是 上的点,且
上的点,且
 .将
.将 沿
沿 折起到
折起到 的位置,使
的位置,使 ,如图2.
,如图2.
(Ⅰ) 是
是 的中点,求
的中点,求 与平面
与平面 所成角的大小;
所成角的大小;
(Ⅱ)求二面角 的正切值.
的正切值.
(本小题满分12分)已知向量 ,设函数
,设函数 .
.
(Ⅰ)求函数 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(Ⅱ)在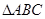 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是 ,若
,若 ,
,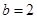 ,
, ,求边
,求边 的长.
的长.
(本小题满分12分)设各项均为正数的数列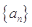 的前
的前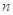 项和为
项和为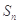 ,满足
,满足
 且
且 构成等比数列.
构成等比数列.
(Ⅰ)求数列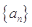 的通项公式;
的通项公式;
(Ⅱ)证明:对一切正整数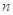 ,有
,有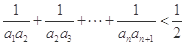 .
.
(本小题满分14分)设函数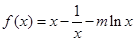 .
.
(Ⅰ)若函数 在定义域上为增函数,求实数
在定义域上为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)在(Ⅰ)的条件下,若函数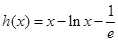 ,
, 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.