(本小题满分12分)
已 知椭圆
知椭圆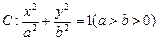 的离心率为
的离心率为 其左、右焦
其左、右焦 点分别为
点分别为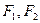 ,点P是坐标平面内一点,且
,点P是坐标平面内一点,且 (O为坐标原点)。
(O为坐标原点)。
(1)求椭圆C的方程;
(2) 过点
过点 且斜率为k的动直线
且斜率为k的动直线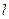 交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出M的坐标;若不存在,说明理由。
交椭圆于A、B两点,在y轴上是否存在定点M,使以AB为直径的圆恒过这个点?若存在,求出M的坐标;若不存在,说明理由。

如图,四面体ABCD中,O是BD的中点,ΔABD和ΔBCD均为等边三角形,
AB ="2" ,AC = .
.
(I)求证: 平面BCD;
平面BCD;
(II)求二面角A-BC- D的大小;
(III)求O点到平面ACD的距离.
已知向量a ,向量b
,向量b ,若
,若 a·b +1 .
a·b +1 .
(I)求函数 的解析式和最小正周期;
的解析式和最小正周期;
(II) 若 ,求
,求 的最大值和最小值.
的最大值和最小值.
已知:
(1)若
(2)若 的最大值和最小值和为3,求
的最大值和最小值和为3,求 的值.
的值.
在直三棱柱 中,
中,
|
(1)求证:
 的大小;
的大小;

把圆周分成四等份,A是其中一个分点,动点P在四个分点上按逆时针方向前进。现在投掷一个质地均匀的正四面体,它的四个面上分别写有1、2、3、4四个数字。P从A点出发,按照正四面体底面上数字前进几个分点,转一周之前连续投掷.
(1)求点P恰好返回A点的概率;
(2)在点P转一周恰能返回A点的所有结果中,用随即变量 表示点P能返回A点的投掷次数,求
表示点P能返回A点的投掷次数,求 的分数列和期望.
的分数列和期望.