((本小题满分14分)
已知两点M(-1,0),N(1,0),且点P使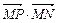 ,
, ,
,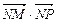 成公差小于零的等差数列。
成公差小于零的等差数列。
(1)点P的轨迹是什么曲线?
(2)若点P的坐标为(x0,y0),记为θ为 的夹角,求tanθ.
的夹角,求tanθ.
袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为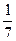 ,现有甲、乙两人从袋中轮流摸取1球.甲先取,乙后取,然后甲再取…取后不放回,每人最多取两次,若两人中有一人首先取到白球时则终止,每个球在每一次被取出的机会是等可能的.
,现有甲、乙两人从袋中轮流摸取1球.甲先取,乙后取,然后甲再取…取后不放回,每人最多取两次,若两人中有一人首先取到白球时则终止,每个球在每一次被取出的机会是等可能的.
(1)求袋中原有白球的个数;
(2)求甲取到白球的概率;
(3)求取球4次终止的概率.
已知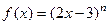 展开式的二项式系数和为512,
展开式的二项式系数和为512,
且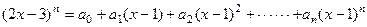
(1)求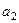 的值;
的值;
(2)求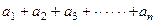 的值;
的值;
(3)求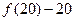 被6整除的余数.
被6整除的余数.
某同学练习投篮,已知他每次投篮命中率为 ,
,
(1)求在他第三次投篮后,首次把篮球投入篮框内的概率;
(2)若想使他投入篮球的概率达到0.99,则他至少需投多少次?(lg2=0.3)
(本小题满分14分)已知函数 ,
,
(1)若函数 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;
(2)令 ,是否存在实数
,是否存在实数 ,当
,当
 (
( 是自然常数)时,函数
是自然常数)时,函数 的最小值是3,若存在,求出
的最小值是3,若存在,求出 的值;若不存在,说明理由。K
的值;若不存在,说明理由。K
(本小题满分12分)
已知 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间 上是减函数,
上是减函数,
又
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若在区间 (m>0)上恒有
(m>0)上恒有 ≤
≤ x成立,求m的取值范围。
x成立,求m的取值范围。