.(本小题满分12分)
如图,四面体ABCD中,O是BD的中点,△ABD和△BCD均为等边三角形,AB=2,AC=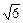
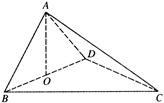
(1)求证:AO⊥平面BCD;
(2)求二面角A—BC—D的余弦值;
(3)求点O到平面ACD的距离.
如图,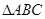 的角平分线AD的延长线交它的外接圆于点E
的角平分线AD的延长线交它的外接圆于点E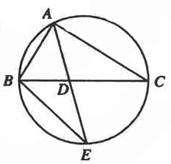
(Ⅰ)证明: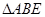


(Ⅱ)若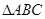 的面积
的面积 ,求
,求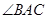 的大小。
的大小。
已知函数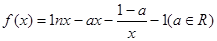 .
.
(Ⅰ)当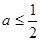 时,讨论
时,讨论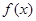 的单调性;
的单调性;
(Ⅱ)设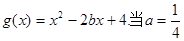 时,若对任意
时,若对任意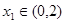 ,存在
,存在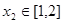 ,使
,使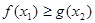 ,求实数
,求实数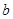 的取值范围.
的取值范围.
设椭圆C: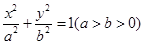 的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,
的左焦点为F,过点F的直线与椭圆C相交于A,B两点,直线l的倾斜角为60o,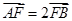 .
.
求椭圆C的离心率;
如果|AB|=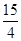 ,求椭圆C的方程.
,求椭圆C的方程.
已知等差数列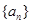 的前
的前 项和为
项和为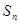 ,且
,且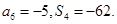
(1)求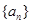 通项公式;
通项公式;
(2)求数列 的前
的前 项和
项和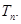
如图,某观测站C在城A的南偏西 的方向,从城A出发有一条走向为南偏东
的方向,从城A出发有一条走向为南偏东 的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?
的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,这时此车距离A城多少千米?