(本小题满分12分)
已知双曲线 的离心率
的离心率 ,其一条准线方程为
,其一条准线方程为 .
.
(Ⅰ)求双曲线 的方程;
的方程;
(Ⅱ)如题20图:设双曲线 的左右焦点分别为
的左右焦点分别为 ,点
,点 为该双曲线右支上一点,直线
为该双曲线右支上一点,直线 与其左支 交于点
与其左支 交于点 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)数列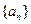 是首项
是首项 的等比数列,且
的等比数列,且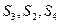 成等差数列.
成等差数列.
(I)求数列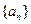 的通项公式;
的通项公式;
(II)设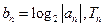 为数列
为数列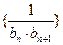 的前
的前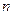 项和,求
项和,求 .
.
(本小题满分10分) 设命题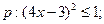 命题
命题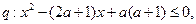 若
若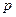 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数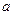 的取值范围.
的取值范围.
已知数列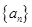 的前
的前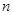 项和为
项和为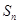 ,且
,且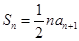 (
(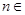 N*),其中
N*),其中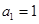 .
.
(Ⅰ)求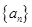 的通项公式;
的通项公式;
(Ⅱ) 设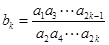 (
(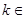 N*).
N*).
①证明: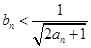 ;
;
② 求证: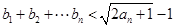 .
.
已知点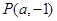 (
(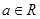 ),过点
),过点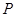 作抛物线
作抛物线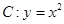 的切线,切点分别为
的切线,切点分别为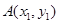 、
、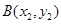 (其中
(其中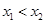 ).
).
(Ⅰ)求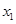 与
与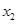 的值(用
的值(用 表示);
表示);
(Ⅱ)若以点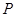 为圆心的圆
为圆心的圆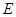 与直线
与直线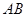 相切,求圆
相切,求圆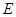 面积的最小值.
面积的最小值.
某学校拟建一座长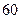 米,宽
米,宽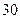 米的长方形体育馆.按照建筑要求,每隔
米的长方形体育馆.按照建筑要求,每隔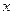 米需打建一个桩位,每个桩位需花费
米需打建一个桩位,每个桩位需花费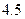 万元(桩位视为一点且打在长方形的边上),桩位之间的
万元(桩位视为一点且打在长方形的边上),桩位之间的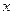 米墙面需花
米墙面需花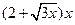 万元,在不计地板和天花板的情况下,当
万元,在不计地板和天花板的情况下,当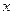 为何值时,所需总费用最少?
为何值时,所需总费用最少?