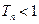设函数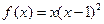 ,
, .
.
⑴求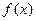 的极值;
的极值;
(2)设函数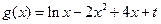 (
( 为常数),若使
为常数),若使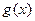 ≤
≤ ≤
≤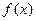 在
在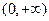 上恒成立的实数
上恒成立的实数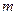 有且只有一个,求实数
有且只有一个,求实数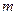 和
和 的值;
的值;
(3)讨论方程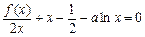 的解的个数,并说明理由.
的解的个数,并说明理由.
在数列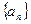 中,
中,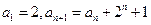
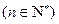 .
.
(Ⅰ)求证:数列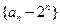 为等差数列;
为等差数列;
(Ⅱ)设数列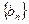 满足
满足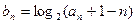 ,若
,若
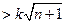 对一切
对一切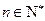 且
且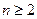 恒成立,求实数
恒成立,求实数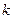 的取值范围
的取值范围
已知函数 在
在 上为增函数,其中
上为增函数,其中 ,
,
(1)求 的取值集合;
的取值集合;
(2) ,若
,若 在
在 上为单调函数,求m的取值范围.
上为单调函数,求m的取值范围.
如图,某人在塔的正东方向上的C处在与塔垂直的水平面内沿南偏西60°的方向以每小时6千米的速度步行了1分钟以后,在点D处望见塔的底端B在东北方向上,已知沿途塔的仰角
 ,
, 的最大值为
的最大值为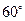 .
.
(1)求该人沿南偏西60°的方向走到仰角 最大时,走了几分钟;
最大时,走了几分钟;
(2)求塔的高AB.
已知数列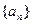 满足条件:
满足条件: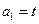 ,
,
(1)判断数列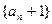 是否为等比数列;
是否为等比数列;
(2)若 ,令
,令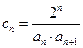 ,
,
证明:(1) ;(2)
;(2)