已知两条直线 与
与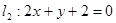 的交点P,
的交点P,
(1)求过点P且平行于直线 的直线
的直线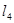 的方程;
的方程;
(2)若直线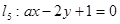 与直线
与直线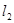 垂直,求
垂直,求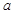 .
.
已知直线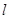 经过点(0,-2),其倾斜角是60°.
经过点(0,-2),其倾斜角是60°.
(1)求直线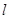 的方程;(2)求直线
的方程;(2)求直线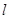 与两坐标轴围成三角形的面积
与两坐标轴围成三角形的面积
已知椭圆的两个焦点分别为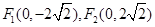 ,离心率
,离心率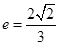 .
.
(1)求椭圆的方程.
(2)一条不与坐标轴平行的直线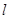 与椭圆交于不同的两点
与椭圆交于不同的两点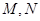 ,且线段
,且线段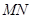 的中点的横坐标为
的中点的横坐标为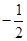 ,求直线
,求直线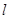 的斜率的取值范围.
的斜率的取值范围.
已知p :A={x∣2a≤x≤a2+1},q: B={x∣x2-3(a +1)x+2(3a+1) ≤ 0}。若p是q的充分条件,求实数a的取值范围
等差数列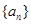 的各项均为正数,
的各项均为正数,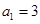 ,前
,前 项和为
项和为 ,
,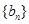 为等比数列,
为等比数列, 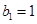 ,且
,且
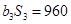 .
.
(1)求 与
与 ; (2)求和:
; (2)求和: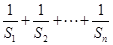 .
.