设定义在区间[x1,x2]上的函数y=f(x)的图象为C,M是C上的任意一点,O为坐标原点,设向
量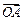 =
=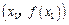 ,
,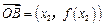 ,
,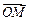 =(x,y),当实数λ满足x="λ" x1+(1-λ) x2时,记向
=(x,y),当实数λ满足x="λ" x1+(1-λ) x2时,记向
量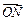 =λ
=λ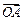 +(1-λ)
+(1-λ)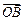 .定义“函数y=f(x)在区间[x1,x2]上可在标准k下线性近似”是指
.定义“函数y=f(x)在区间[x1,x2]上可在标准k下线性近似”是指
“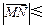 k恒成立”,其中k是一个确定的正数.
k恒成立”,其中k是一个确定的正数.
(1)设函数 f(x)=x2在区间[0,1]上可在标准k下线性近似,求k的取值范围;
(2)求证:函数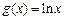 在区间
在区间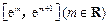 上可在标准k=
上可在标准k=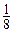 下线性近似.
下线性近似.
(参考数据:e =2.718,ln(e-1)=0.541)
=2.718,ln(e-1)=0.541)
已知命题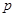 :方程
:方程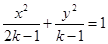 表示椭圆;
表示椭圆; :方程
:方程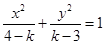 表示双曲线. 若“
表示双曲线. 若“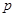 或
或 ”为真,“
”为真,“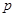 且
且 ” 为假,求实数
” 为假,求实数 的取值范围.
的取值范围.
如图, 中
中 ,平面
,平面 外一条线段AB满足AB∥DE,AB
外一条线段AB满足AB∥DE,AB ,AB⊥AC,F是CD的中点.
,AB⊥AC,F是CD的中点.
(1)求证:AF∥平面BCE
(2)若AC=AD,证明:AF⊥平面
某校在一次趣味运动会的颁奖仪式上,高一、高二、高三各代表队人数分别为120人、120人、n人.为了活跃气氛,大会组委会在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取20人在前排就坐,其中高二代表队有6人.
(1)求n的值;
(2)把在前排就坐的高二代表队6人分别记为a,b,c,d,e,f,现随机从中抽取2人上台抽奖,.求a和b至少有一人上台抽奖的概率;
已知椭圆 的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,直线
的离心率互为倒数,直线 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(1)求椭圆 的方程;
的方程;
(2)设椭圆 的左焦点为
的左焦点为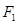 ,右焦点为
,右焦点为 ,直线
,直线 过点
过点 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线 垂直
垂直 于点
于点 ,线段
,线段 垂直平分线交
垂直平分线交 于点
于点 ,求点
,求点 的轨迹
的轨迹 的方程;
的方程;
(3)设第(2)问中的 与
与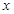 轴交于点
轴交于点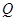 ,不同的两点
,不同的两点 在
在 上,且满足
上,且满足 ,求
,求 的取值范围.
的取值范围.
如图,已知四棱锥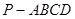 中,底面
中,底面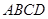 为菱形,
为菱形, 平面
平面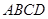 ,
, ,
,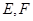 分别是
分别是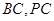 的中点.
的中点.
(1)证明: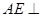 平面
平面 ;
;
(2)取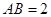 ,若
,若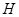 为
为 上的动点,
上的动点, 与平面
与平面 所成最大角的正切值为
所成最大角的正切值为 ,求二面角
,求二面角 的余弦值。
的余弦值。