已知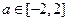 ,
,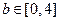 ,
,
(1)若 ,求事件A:
,求事件A: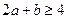 的概率;
的概率;
(2)求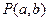 满足条件:
满足条件: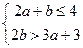 的概率
的概率
(1)推导 关于
关于 的表达式;
的表达式;
(2)利用(1)的结论求 的值.
的值.
已知等比数列的首项为 ,公比为
,公比为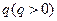 ,前
,前 项和为
项和为 ,其中最大的一项为
,其中最大的一项为 ,又它的前
,又它的前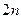 项和为
项和为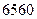 ,求首项
,求首项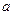 和公比
和公比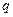 .
.
(本小题满分12分)
数列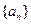 满足
满足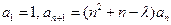 ,
,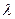 是常数.
是常数.
(1)数列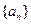 是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
(2)求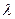 的取值范围,使得存在正整数
的取值范围,使得存在正整数 ,当
,当 时总有
时总有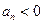 .
.
(本小题满分12分)
已知 、
、 分别是直线
分别是直线 和
和 上的两个动点,线段
上的两个动点,线段 的长为
的长为 ,
, 是
是 的中点.
的中点.
(1)求动点 的轨迹
的轨迹 的方程;
的方程;
(2)过点 作直线
作直线 (与
(与 轴不垂直)与轨迹
轴不垂直)与轨迹 交于
交于 两点,与
两点,与 轴交于点
轴交于点 .若
.若 ,
, ,证明:
,证明: 为定值.
为定值.
(本小题满分12分)
已知函数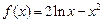
(1)若方程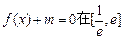 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
(2) 如果函数
如果函数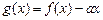 的图象与x轴交于两点
的图象与x轴交于两点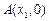 、
、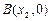 且
且 .求证:
.求证: (其中正常数
(其中正常数 ).
).