如图，矩形ABCD内接于由函数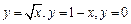
图象围成的封闭图形，其中顶点C，D在
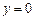上，求矩形ABCD面积的最大值.
(1) 求不等式的解集：
(2)求函数的定义域：
已知直线
（1）当
时，求
与
的交点坐标；
（2）过坐标原点O作的垂线，垂足为A，P为OA的中点，当
变化时，求P点的轨迹的参数方程，
（3）并指出它是什么曲线。
在平面直角坐标系xoy中，已知曲线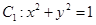
，将
上的所有点的横坐标、纵坐标分别伸长为原来的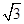
、2倍后得到曲线
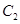，以平面直角坐标系xoy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线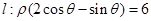
（1）试写出直线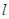
的直角坐标方程；
（2）在曲线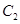上求一点P，使点P到直线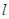的距离最大，并求出此最大值。
已知圆的方程为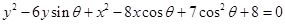
（1）求圆心轨迹C的参数方程;
（2）点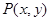
是（1）中曲线C上的动点，求
的取值范围。
从极点O作直线和直线
相交于点M，在OM上取一点P,使
,求点P的轨迹的极坐标方程。