已知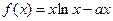 ,
,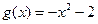 ,
,
(Ⅰ)对一切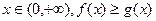 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅱ)当 求函数
求函数 (
(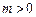 )上的最小值.
)上的最小值.
(本题满分12分)
已知向量


 ,函数
,函数
 ·
· ,
,
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)如果△ABC的三边a、b、c满足 ,且边b所对的角为
,且边b所对的角为 ,试求
,试求 的范围及函数
的范围及函数 的值域.
的值域.
(本题满分14分)
已知二次函数 的图像过点
的图像过点 ,且
,且 ,
, .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)若数列 满足
满足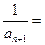
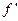
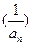 ,且
,且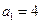 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)记 ,数列
,数列 的前
的前 项和
项和 ,求证:
,求证: .
.
(本题满分14分)
如图,三角形ABC中,AC=BC= ,ABED是边长为1
,ABED是边长为1
的正方形,平面ABED⊥底面ABC,若G、F分别是EC、BD的中点.
(Ⅰ)求证:GF//底面ABC;
(Ⅱ)求证:AC⊥平面EBC;
(Ⅲ)求几何体ADEBC的体积V.
(本题满分14分)
甲乙二人用4张扑克牌(分别是红桃2,红桃3,红桃4,方片4)玩游戏,他们将扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张.
(Ⅰ)设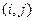 表示甲乙抽到的牌的数字,(如甲抽到红桃2,乙抽到红桃3,记为(2,3))写出甲乙二人抽到的牌的所有情况;
表示甲乙抽到的牌的数字,(如甲抽到红桃2,乙抽到红桃3,记为(2,3))写出甲乙二人抽到的牌的所有情况;
(Ⅱ)若甲抽到红桃3,则乙抽出的牌面数字比3大的概率是多少?
(Ⅲ)甲乙约定,若甲抽到的牌的牌面数字比乙大,则甲胜;否则,乙胜,你认为此游戏是否公平?请说明理由.
(本题满分12分)
已知向量

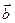
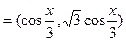 ,函数
,函数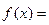
 ·
·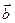 ,
,
(Ⅰ)求函数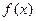 的单调递增区间;
的单调递增区间;
(Ⅱ)如果△ABC的三边a、b、c满足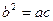 ,且边b所对的角为
,且边b所对的角为 ,试求
,试求 的范围及函数
的范围及函数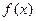 的值域.
的值域.