(本题满分12分)
已知向量

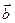
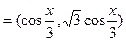 ,函数
,函数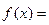
 ·
·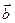 ,
,
(Ⅰ)求函数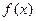 的单调递增区间;
的单调递增区间;
(Ⅱ)如果△ABC的三边a、b、c满足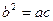 ,且边b所对的角为
,且边b所对的角为 ,试求
,试求 的范围及函数
的范围及函数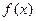 的值域.
的值域.
(本小题满分13分) 已知一拱桥的桥孔为抛物线型且桥孔顶点距水面2米时,测量桥孔水面宽为8米,一船宽5米,高1米,能否通过拱桥的桥孔?请用计算的方法给予说明。
(本小题满分13分)已知p: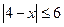 ,q:
,q: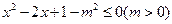 ,若非p是非q的必要而不充分条件,求实数m的取值范围.
,若非p是非q的必要而不充分条件,求实数m的取值范围.
(本小题满分13分)已知椭圆的对称轴为坐标轴且焦点在x轴,离心率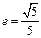 ,短轴长为4,(1)求椭圆的方程;
,短轴长为4,(1)求椭圆的方程;
(2)过椭圆的右焦点作一条斜率为2的直线与椭圆交于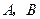 两点,求AB的中点坐标及其弦长|AB|。
两点,求AB的中点坐标及其弦长|AB|。
(本小题满分13分)已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3)。
(1)求AB边上的高线所在的直线方程;(2)求三角形ABC的面积。
(本小题满分16分)
已知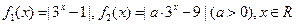 ,
,
且 .
.
(Ⅰ)当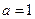 时,求
时,求 在
在 处的切线方程;
处的切线方程;
(Ⅱ)当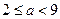 时,设
时,设 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为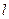 (闭区间
(闭区间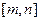 的长度定义为
的长度定义为 ),试求
),试求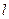 的最大值;
的最大值;
(Ⅲ)是否存在这样的 ,使得当
,使得当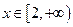 时,
时, ?若存在,求出
?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.