已知椭圆 :
: (
( ),其焦距为
),其焦距为 ,若
,若 (
( ),则称椭圆
),则称椭圆 为“黄金椭圆”.
为“黄金椭圆”.
(1)求证:在黄金椭圆 :
: (
( )中,
)中, 、
、 、
、 成等比数列.
成等比数列.
(2)黄金椭圆 :
: (
( )的右焦点为
)的右焦点为 ,
, 为椭圆
为椭圆 上的
上的
任意一点.是否存在过点 、
、 的直线
的直线 ,使
,使 与
与 轴的交点
轴的交点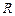 满足
满足 ?若存在,求直线
?若存在,求直线 的斜率
的斜率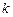 ;若不存在,请说明理由.
;若不存在,请说明理由.
(3)在黄金椭圆中有真命题:已知黄金椭圆 :
: (
( )的左、右焦点分别是
)的左、右焦点分别是 、
、 ,以
,以 、
、 、
、 、
、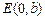 为顶点的菱形
为顶点的菱形 的内切圆过焦点
的内切圆过焦点 、
、 .试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
.试写出“黄金双曲线”的定义;对于上述命题,在黄金双曲线中写出相关的真命题,并加以证明.
(本小题满分12分)某工厂生产 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
 |
7 |
7 |
7.5 |
9 |
9.5 |
 |
6 |
 |
8.5 |
8.5 |
 |
由于表格被污损,数据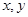 看不清,统计员只记得
看不清,统计员只记得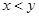 ,且
,且 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(1)求表格中 与
与 的值;
的值;
(2)若从被检测的5件B种元件中任取2件,求2件都为正品的概率.
(本小题满分12分)在三角形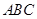 中,
中,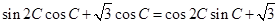 .
.
(1)求角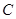 的大小;
的大小;
(2)若 ,且
,且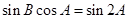 ,求
,求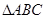 的面积.
的面积.
(本小题满分10分)已知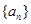 为等比数列,其中
为等比数列,其中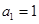 ,且
,且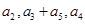 成等差数列.
成等差数列.
(1)求数列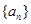 的通项公式;
的通项公式;
(2)设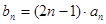 ,求数列
,求数列 的前
的前 项和
项和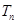 .
.
(本小题14分)设函数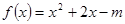 ,
,
(1)当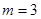 时,求函数f(x)的零点;
时,求函数f(x)的零点;
(2)当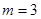 时,判断
时,判断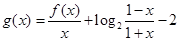 的奇偶性并给予证明;
的奇偶性并给予证明;
(3)当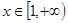 时,
时,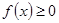 恒成立,求
恒成立,求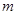 的最大值.
的最大值.
(本小题满分14分)某租凭公司拥有汽车100辆,当每辆汽车的月租为3000元时,可全部租出,当每辆车的月租金增加50元时,未租出的车辆会增加一辆,租出的车每辆每月需要维护费150元,未租出的车每月需要维护费50元。
(1)当每辆车的月租金定位3600时,能租出多少辆车?
(2)当每辆车的月租金定位多少钱时,租凭公司的月收益最大?最大收益是多少?