(本小题满分12分)在三角形 中,
中,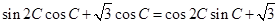 .
.
(1)求角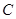 的大小;
的大小;
(2)若 ,且
,且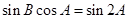 ,求
,求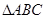 的面积.
的面积.
(本小题满分13分) 已知直线
已知直线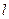 与函数
与函数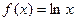 的图象相切于点
的图象相切于点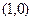 ,且
,且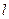 与函数
与函数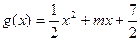
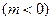 的图象也相切.
的图象也相切.
求(Ⅰ)求直线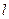 的方程及m的值;
的方程及m的值;
(Ⅱ)设 ,若
,若 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(本小题满分13分)
椭圆C: 的离心率为
的离心率为 ,且过点(2,0)
,且过点(2,0)
(1)求椭圆C的方程;
(2)设直线 :
: 与椭圆C交于A、B两点,O为坐标原点,若
与椭圆C交于A、B两点,O为坐标原点,若 OAB为直角三角形,求
OAB为直角三角形,求 的值。
的值。
(本小题满分12分)如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分PC,且分别交AC、PC于D、E两点,又PB=BC,PA=AB.
(Ⅰ)求证:PC⊥平面BDE;
(Ⅱ)若点Q是线段PA上任一点,求证:BD⊥DQ;
(Ⅲ)线段PA上是否存在点Q,使得PC//平面BDQ.若存在,求出 点的位置,若不存在,说明理由.
点的位置,若不存在,说明理由.
(本小题满分12分)为了了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下: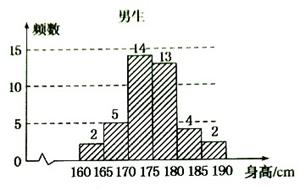
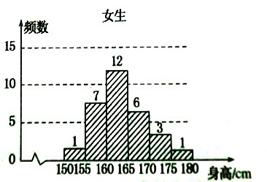
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,
求至少有1人身高在185~190cm之间的概率。
(本小题满分12分)已知函数 ,
,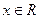
(1)求函数 的最大值及对应的
的最大值及对应的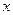 的取值集合;
的取值集合;
(2)在给定的坐标系中,画出函数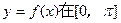 上的图象。
上的图象。