(本小题满分12分)某工厂生产 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
 |
7 |
7 |
7.5 |
9 |
9.5 |
 |
6 |
 |
8.5 |
8.5 |
 |
由于表格被污损,数据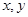 看不清,统计员只记得
看不清,统计员只记得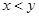 ,且
,且 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.
(1)求表格中 与
与 的值;
的值;
(2)若从被检测的5件B种元件中任取2件,求2件都为正品的概率.
已知函数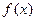 的定义域为
的定义域为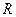 ,并满足(1)对于一切实数
,并满足(1)对于一切实数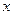 ,都有
,都有 ;
;
(2)对任意的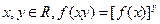 ; (3)
; (3) ;
;
利用以上信息求解下列问题:
(1)求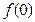 ;
;
(2)证明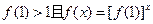 ;
;
(3)若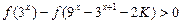 对任意的
对任意的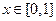 恒成立,求实数
恒成立,求实数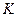 的取值范围。
的取值范围。
已知函数
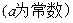
(1)是否存在实数 ,使函数
,使函数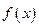 是
是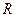 上的奇函数,若不存在,说明理由,若存在实数
上的奇函数,若不存在,说明理由,若存在实数 ,求函数
,求函数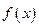 的值域;
的值域;
(2)探索函数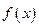 的单调性
的单调性 ,并利用定义加以证明。
,并利用定义加以证明。
二次函数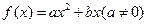 ,满足
,满足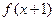 为偶函数,且方程
为偶函数,且方程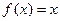 有相等实根。
有相等实根。
(1)求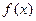 的解析式;
的解析式;
(2)求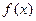 在
在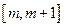 上的最大值。
上的最大值。
某商家经销一种销售成本 为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,针对这种销售情况,
为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg,针对这种销售情况,
(1)设销售单价为每千克x元,月销售利润 为y元,求y与x的函数关系式;
为y元,求y与x的函数关系式;
商店想在月销售成本不超过10000元的情况下,使得月销售利润不少于8000元,销售单价应定为多少元时,利润最大?
已知函数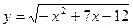 的定义域是
的定义域是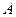 ,函数
,函数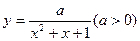 在
在 上的值域为
上的值域为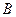 ,全集为
,全集为 ,且
,且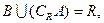 求实数
求实数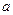 的取值范围。
的取值范围。