(本小题满分12分)函数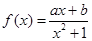 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.
(1)求实数 的值.(2)用定义证明
的值.(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值(无需说明理由).
有无最大值或最小值?如有,写出最大值或最小值(无需说明理由).
(1)二次函数 满足:
满足: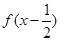 为偶函数且
为偶函数且 ,求
,求 的解析式;
的解析式;
(2)若函数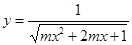 定义域为
定义域为 ,求
,求 取值范围。
取值范围。
(3)若函数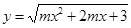 值域为
值域为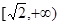 ,求
,求 取值范围。
取值范围。
(4)若函数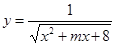 在
在 上单调递减,求
上单调递减,求 取值范围。
取值范围。
(本小题满分12分)已知函数 .(1)将函数
.(1)将函数 的解析式写成分段函数;
的解析式写成分段函数;
(2)在给出的坐标系中画出 的图象,并根据图象写出函数
的图象,并根据图象写出函数 的单调区间和值域.
的单调区间和值域.
已知数列 的前
的前 项和为
项和为 ,且
,且 对一切正整数
对一切正整数 都成立.
都成立.
(1)求 ,
, 的值;
的值;
(2)设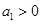 ,数列
,数列 的前
的前 项和为
项和为 ,当
,当 为何值时,
为何值时, 最大?并求出
最大?并求出 的最大值.
的最大值.
(12分)函数 在一个周期内的图象如图所示,
在一个周期内的图象如图所示, 为图象的最高点,
为图象的最高点, 、
、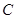 为图象与
为图象与 轴的交点,且
轴的交点,且 为正三角形.
为正三角形.
(1)求 的值及函数
的值及函数 的值域;
的值域;
(2)若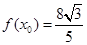 ,且
,且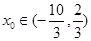 ,求
,求 的值.
的值.