已知函数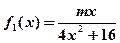
,
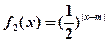（其中
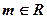且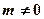
）.
（1）讨论函数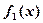
的单调性；
（2）若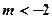
，求函数
,
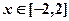的最值；
（3）设函数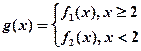
,当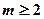
时，若对于任意的
，总存在唯一
的
，使得
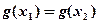成立．试求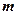
的取值范围．
定义在D上的函数f(x)，如果满足：对任意x∈D，存在常数M>0，都有|f(x)|≤M成立，则称f(x)是D上的有界函数，其中M称为函数f(x)的上界．已知函数f(x)＝1＋a·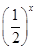
＋
.
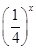(1)当a＝1时，求函数f(x)在(－∞，0)上的值域，并判断函数f(x)在(－∞，0)上是否为有界函数，请说明理由；
(2)若函数f(x)在[0，＋∞)上是以3为上界的有界函数，求实数a的取值范围．
已知f(x)＝xlnx，g(x)＝－x2＋ax－3.
(1)求函数f(x)在[t，t＋2](t>0)上的最小值；
(2)对一切x∈(0，＋∞)，2f(x)≥g(x)恒成立，求实数a的取值范围；
(3)证明对一切x∈(0，＋∞)，都有lnx>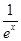
－
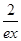成立．
设函数f(x)＝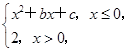
其中b>0，c∈R.当且仅当x＝－2时，函数f(x)取得最小值－2.
(1)求函数f(x)的表达式；
(2)若方程f(x)＝x＋a(a∈R)至少有两个不相同的实数根，求a取值的集合．
已知函数f(x)＝ax2－|x|＋2a－1(a为实常数)．
(1)若a＝1，作函数f(x)的图象；
(2)设f(x)在区间[1，2]上的最小值为g(a)，求g(a)的表达式；
(3)设h(x)＝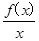
，若函数h(x)在区间[1，2]上是增函数，求实数a的取值范围．
已知函数f(x)＝lg(1－x)＋lg(1＋x)＋x4－2x2.
(1)求函数f(x)的定义域；
(2)判断函数f(x)的奇偶性；
(3)求函数f(x)的值域．