如图,已知椭圆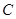 的中心在原点,其一个焦点与抛物线
的中心在原点,其一个焦点与抛物线 的焦点相同,又椭圆
的焦点相同,又椭圆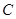 上有一点
上有一点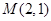 ,直线
,直线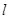 平行于
平行于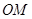 且与椭圆
且与椭圆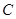 交于
交于 两点,连
两点,连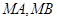
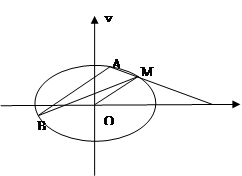
(Ⅰ)求椭圆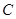 的方程;
的方程;
(Ⅱ)当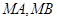 与
与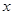 轴所构成的三角形是以
轴所构成的三角形是以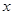 轴上所在线段为底边的等腰三角形时,求直线
轴上所在线段为底边的等腰三角形时,求直线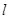 在
在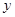 轴上截距的取值范围.
轴上截距的取值范围.
已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,ω>0,0<φ< )的周期为π,且图象上一个最低点为M
)的周期为π,且图象上一个最低点为M .
.
(1)求f(x)的解析式;
(2)当x∈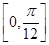 时,求f(x)的最值.
时,求f(x)的最值.
已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ< )的周期为π,且图象上有一个最低点为M
)的周期为π,且图象上有一个最低点为M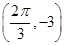 .
.
(1)求f(x)的解析式;
(2)求函数y=f(x)+f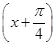 的最大值及对应x的值.
的最大值及对应x的值.
已知f(x)=cos(ωx+φ)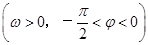 的最小正周期为π,且f
的最小正周期为π,且f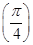 =
=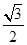 .
.
(1)求ω和φ的值;
(2)在给定坐标系中作出函数f(x)在[0,π]上的图象;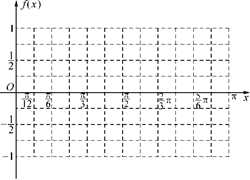
(3)若f(x)> ,求x的取值范围.
,求x的取值范围.
已知a=(2cosx,cos2x),b=(sinx,-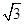 ),f(x)=a·b.
),f(x)=a·b.
(1)求f(x)的振幅、周期,并画出它在一个周期内的图象;
(2)说明它可以由函数y=sinx的图象经过怎样的变换得到.
已知函数f(x)=2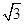 ·sin
·sin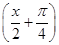 cos
cos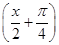 -sin(x+π).
-sin(x+π).
(1)求f(x)的最小正周期;
(2)若将f(x)的图象向右平移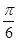 个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.