


(本题满分13分,第(Ⅰ)问4分,第(Ⅱ)问4分, 第(Ⅲ)问5分)
甲、乙 两人独立地破译一个密码,他们能译出密码的概率分别为 ,求:
,求:
(Ⅰ)两个人都能译出密码的概率;
(Ⅱ)恰有一个人译出密码的概率;
(Ⅲ)至多有一个人译出密码的概率.
(本小题满分12分)已知双曲线 的两条渐近线与抛物线
的两条渐近线与抛物线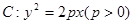 的准线分别交于A, B两点, O为坐标原点.若双曲线的离心率为2, △AOB的面积为
的准线分别交于A, B两点, O为坐标原点.若双曲线的离心率为2, △AOB的面积为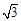 .
.
(1)求抛物线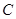 的方程;
的方程;
(2)过点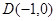 的直线
的直线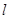 与抛物线
与抛物线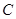 交于不同的两点
交于不同的两点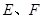 ,若在
,若在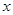 轴上存在一点
轴上存在一点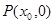 使得
使得 是等边三角形,求
是等边三角形,求 的值.
的值.
(本小题满分12分)在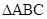 中,角
中,角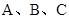 的对边分别为
的对边分别为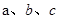 ,若
,若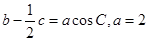 .
.
(1)求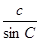 的值;
的值;
(2)若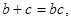 求
求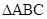 的面积.
的面积.
如图,直三棱柱(侧棱垂直于底面)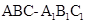 中,
中,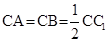 ,点
,点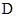 是棱
是棱 的中点,且
的中点,且 .
.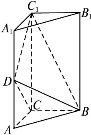
(1)求证: ;
;
(2)求直线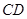 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分12分)从一批苹果中随机抽取100个作为样本,其重量(单位:克)的频数分布表如下:
| 分组(重量) |
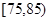 |
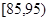 |
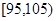 |
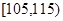 |
| 频数(个) |
15 |
30 |
35 |
20 |
(1)在频率分布直方图中,求分组重量在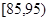 对应小矩形的高;
对应小矩形的高;
(2)利用频率估计这批苹果重量的平均数.
(3)用分层抽样的方法从重量在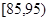 和
和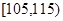 的苹果中抽取5个,从这5个苹果任取2个,求重量在这两个组中各有1个的概率.
的苹果中抽取5个,从这5个苹果任取2个,求重量在这两个组中各有1个的概率.