某商场将进价为30元的书包以40元售出,平均每月能售出600个,调查表明:这种书包的售价每上涨1元,其销售量就减少10个。
(1)请写出每月售出书包的利润y元与每个书包涨价x元间的函数关系式;
(2)设每月的利润为10000的利润是否为该月最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时书包的售价应定为多少元。
(3)请分析并回答售价在什么范围内商家就可获得利润。
某电脑经销商计划同时购进一批电脑机箱和液晶显示器,若购进电脑机箱10台和液晶显示器8台,共需要资金7000元;若购进电脑机箱2台和液晶显示器5台,共需要资金4120元.
(1)每台电脑机箱、液晶显示器的进价各是多少元?
(2)该经销商计划购进这两种商品共50台,而可用于购买这两种商品的资金不超过22240元.根据市场行情,销售电脑机箱、液晶显示器一台分别可获利10元和160元.该经销商希望销售完这两种商品,所获利润不少于4100元.试问:该经销商有哪几种进货方案?哪种方案获利最大?最大利润是多少?
关于x的方程kx2+(k+2)x+ =0有两个不相等的实数根.
=0有两个不相等的实数根.
(1)求k的取值范围;
(2)当k=4时方程的两根分别为x1 、x2,直接写出x1 +x2 ,x1 x2的值;
(3)是否存在实数k使方程的两个实数根的倒数和等于0?若存在,求出k的值,若不存在,说明理由。
某景区有一个景观奇异的天门洞,D点是洞的入口,游人从入口进洞游览后,可经山洞到达山顶的出口凉亭A处观看旅游区风景,最后坐缆车沿索道AB返回山脚下的B处,在同一平面内,若测得斜坡BD的长为100米,坡角∠DBC =10°,在B处测得A的仰角∠ABC=40°,在D处测得A的仰角∠ADF=85°,过D点作地面BE的垂线,垂足为C.
(1)求∠ADB的度数:
(2)过D点作AB的垂线,垂足为G,求DG的长及索道AB的长.(结果保留根号)
如图,四边形ABCD的对角线AC与BD相交于O点,∠1=∠2,∠3=∠4.
求证:(1)△ABC≌△ADC;(2)BO=DO.
为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,抽样调查了50名学生参加户外活动的时间,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题: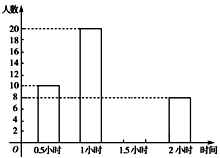
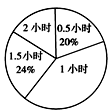
(1)补充户外活动时间为1.5小时的频数分布直方图;
(2)求表示户外活动时间 1小时的扇形圆心角的度数;
(3)户外活动时间的中位数是多少?
(4)本次调查中学生参加户外活动的平均时间是否符合要求?