已知函数f(x)=x3-2x2+ax(x∈R,a∈R),在曲线y=f(x)的所有切线中,有且仅有一条切线l与直线y=x垂直.
(1)求a的值和切线l的方程;
(2)设曲线y=f(x)上任一点处的切线的倾斜角为θ,求θ的取值范围
已知 ,点
,点 在函数
在函数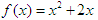 的图象上,其中
的图象上,其中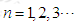
(1)证明:数列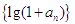 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)记 ,求数列
,求数列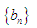 的前
的前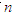 项和
项和 .
.
设函数
(Ⅰ)若 ,解不等式
,解不等式 ;
;
(Ⅱ)若函数 有最小值,求实数
有最小值,求实数 的取值范围.
的取值范围.
已知极坐标系的极点与直角坐标系的原点重合,极轴与直角坐标系的轴的正半轴重合.直线的参数方程是 (为参数),曲线C的极坐标方程为
(为参数),曲线C的极坐标方程为 .
.
(Ⅰ)求曲线C的直角坐标方程;
(Ⅱ)设直线与曲线C相交于M,N两点,求M,N两点间的距离.
如图,△ 内接于⊙
内接于⊙ ,
, ,直线
,直线 切⊙
切⊙ 于点
于点 ,弦
,弦 ,
, 相交于点
相交于点 .
.
(Ⅰ)求证:△ ≌△
≌△ ;
;
(Ⅱ)若 ,求
,求 长.
长.
已知 ,点B是
,点B是 轴上的动点,过B作AB的垂线
轴上的动点,过B作AB的垂线 交
交 轴于点Q,若
轴于点Q,若 ,
, .
.
(1)求点P的轨迹方程;
(2)是否存在定直线 ,以PM为直径的圆与直线
,以PM为直径的圆与直线 的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。
的相交弦长为定值,若存在,求出定直线方程;若不存在,请说明理由。