已知直线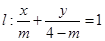
(1)若直线 的斜率等于2,求实数
的斜率等于2,求实数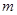 的值;
的值;
(2)若直线 分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最大值及此时直线的方程.
分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最大值及此时直线的方程.
(本小题满分14分)
已知函数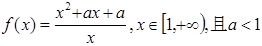
(1)判断 的单调性并证明;
的单调性并证明;
(2)若 满足
满足 ,试确定
,试确定 的取值范围。
的取值范围。
(3)若函数 对任意
对任意 时,
时,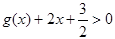 恒成立,求
恒成立,求 的取值范围。
的取值范围。
(本小题满分13分)
已知函数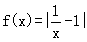
(Ⅰ)判断f(x)在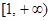 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(Ⅱ)若集合A="{y" | y=f(x),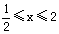 },B=[0,1], 试判断A与B的关系;
},B=[0,1], 试判断A与B的关系;
(本小题满分12分)
已知函数
⑴ 若 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。
⑵ 求 在区间
在区间 上的最小值
上的最小值 的表达式。
的表达式。
(本小题满分12分)
已知f(x)是R上的奇函数,且当x>0时,f(x)=-x2+2x+2.
(1)求f(x)的解析式;
(2)画出f(x)的图象,并指出f(x)的单调区间.
(本小题满分12分)
已知

(1)若a=4,求
(2)若 ,求a的取值范围.
,求a的取值范围.