(本小题满分14分)
已知函数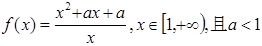
(1)判断 的单调性并证明;
的单调性并证明;
(2)若 满足
满足 ,试确定
,试确定 的取值范围。
的取值范围。
(3)若函数 对任意
对任意 时,
时,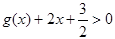 恒成立,求
恒成立,求 的取值范围。
的取值范围。
已知函数f(x)=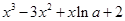 ,曲线
,曲线 在点(0,2)处的切线与
在点(0,2)处的切线与 轴交点的横坐标为-2.
轴交点的横坐标为-2.
(Ⅰ)求a;
(Ⅱ)当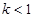 时,曲线
时,曲线 与直线
与直线 只有一个交点,求x的取值范围.
只有一个交点,求x的取值范围.
已知椭圆 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,
直线 与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆C上一点,若过点 的直线
的直线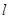 与椭圆C相交于不同的两点S和T,满足
与椭圆C相交于不同的两点S和T,满足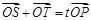 (O为坐标原点),求实数
(O为坐标原点),求实数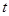 的取值范围.
的取值范围.
心理学家分析发现视觉和空间能力与性别有关, 某数学兴趣小组为了 验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学 (男30女20), 给所有同学几何题和代数题各一题, 让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
(Ⅰ)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(Ⅱ)经过多次测试后,甲每次解答一道几何题所用的时间在5—7分钟,乙每次解答一道几何题所用
的时间在6—8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(Ⅲ)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、 乙两女
生被抽到的人数为X, 求X的分布列及数学期望E(X) .
附表及公式
如图,在四棱锥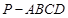 中,底面
中,底面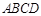 为直角梯形,AD‖BC,
为直角梯形,AD‖BC,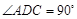 ,平面
,平面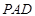 ⊥底面
⊥底面 ,Q为AD的中点,M是棱PC上的点,PA=PD=AD=2,BC=1,CD=
,Q为AD的中点,M是棱PC上的点,PA=PD=AD=2,BC=1,CD=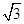 .
.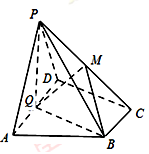
(Ⅰ)求证:平面PQB⊥平面PAD;
(Ⅱ)若二面角M-BQ-C为 ,设PM=t
,设PM=t MC,试确定t的值.
MC,试确定t的值.
设数列{an}满足:a1=1,an+1=3an,n∈N*.设Sn为数列{bn}的前n项和,已知b1≠0,2bn–b1=S1•Sn,n∈N*.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设 ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;
(Ⅲ)证明:对任意n∈N*且n≥2,有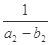 +
+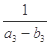 +…+
+…+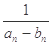 <
<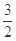 .
.