如图,在四棱锥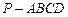 中,侧面
中,侧面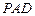
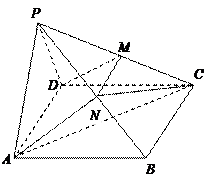
是正三角形,且与底面 垂直,底面
垂直,底面 是边长为2的菱形,
是边长为2的菱形,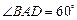 ,
, 是
是 中点,过
中点,过 、
、 、
、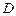 三点的平面交
三点的平面交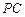 于
于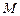 .
.
(1)求证: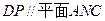 ; (2)求证:
; (2)求证: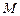 是
是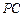 中点;(3)求证:平面
中点;(3)求证:平面 ⊥平面
⊥平面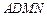 .
.
(本小题满分14分)在锐角 中,角
中,角 所对边分别为
所对边分别为 ,已知
,已知 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,求
,求 的值.
的值.
.已知函数f ( x ) = 3x , f ( a + 2 ) =" 18" , g ( x ) = · 3ax – 4x的定义域为[0,1].
· 3ax – 4x的定义域为[0,1].
(Ⅰ)求a的值;
(Ⅱ)若函数g ( x )在区间[0,1]上是单调递减函数,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知二次函数f(x)满足条件: ,
,
(1)求
(2)讨论 
 的解的个数
的解的个数
(本小题满分12分)已知函数 满足
满足 , 且对于任意
, 且对于任意 ,恒有
,恒有 成立.(1)求实数
成立.(1)求实数 的值;
的值;
(2)解不等式 .
.
(本小题 满分12分)已知 是定义在
是定义在 上的偶函数,且
上的偶函数,且 时,
时, .
.
(1)求 ,
, ;
;
(2)求函数 的表达式;
的表达式;
(3)若 ,求
,求 的取值范围.
的取值范围.