已知直线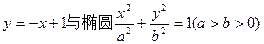 相交于
相交于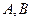 两点,且
两点,且 (其中O为坐标原点).
(其中O为坐标原点).
(1)若椭圆的离心率为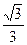 ,求椭圆的标准方程;(2)求证:不论
,求椭圆的标准方程;(2)求证:不论 如何变化,椭圆恒过第一象限内的一个定点
如何变化,椭圆恒过第一象限内的一个定点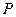 ,并求点
,并求点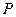 的坐标;(3)若椭圆的离心率
的坐标;(3)若椭圆的离心率 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.
已知 ,且
,且 ∥
∥ .
.
求值:(1) ;
;
(2) .
.
已知不等式 .
.
(1)求该不等式的解集M;
(2)若 ,求证:
,求证:
曲线C的极坐标方程为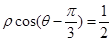 ,以极点O为原点,极轴Ox为x的非负半轴,保持单位长度不变建立直角坐标系xoy.
,以极点O为原点,极轴Ox为x的非负半轴,保持单位长度不变建立直角坐标系xoy.
(1)求曲线C的直角坐标方程;
(2)直线l的参数方程为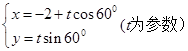 .若C与
.若C与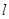 的交点为P,求点P与点A(-2,0)的距离|PA|.
的交点为P,求点P与点A(-2,0)的距离|PA|.
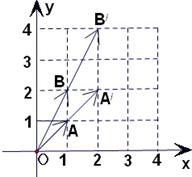
如图,向量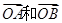 被矩阵M对应的变换
被矩阵M对应的变换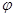 作用后分别变成
作用后分别变成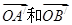 ,
,
(1)求矩阵M;(2)求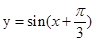 在
在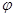 作用后的函数解析式.
作用后的函数解析式.
已知函数f(x)=ln(x+1)+ax2-x,a∈R.
(1)当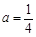 时,求函数y=f(x)的极值;
时,求函数y=f(x)的极值;
(2)是否存在实数b∈(0,1),使得当x∈(-1,b]时,函数f(x)的最大值为f(b)?若存在,求实数a的取值范围,若不存在,请说明理由.