下面玩掷骰子放球的游戏:若掷出1点,甲盒中放入一球;若掷出2点或是3点,乙盒中放入一球;若掷出4点或5点或6点,丙盒中放入一球.设掷n次后,甲、乙、丙盒内的球数分别为x,y,z.
(1)当n=3时,求x、y、z成等差数列的概率;
(2)当n=6时,求x、y、z成等比数列的概率;
(3)设掷4次后,甲盒和乙盒中球的个数差的绝对值为ξ,求Eξ.
在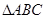 中,
中,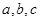 分别为角
分别为角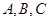 的对边,
的对边,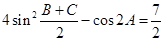 .
.
(1)求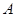 的度数;
的度数;
(2)若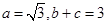 ,求
,求 与
与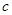 的值.
的值.
已知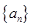 为等差数列,且
为等差数列,且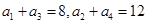 .
.
(1)求数列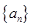 的通项公式;
的通项公式;
(2)记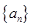 的前
的前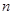 项和为
项和为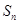 ,若
,若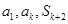 成等比数列,求正整数
成等比数列,求正整数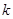 的值.
的值.
已知钝角三角形的三边长分别为2,3,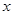 ,则
,则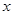 的取值范围.
的取值范围.
对于数列 ,把
,把 作为新数列
作为新数列 的第一项,把
的第一项,把 或
或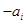 (
( )作为新数列
)作为新数列 的第
的第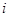 项,数列
项,数列 称为数列
称为数列 的一个生成数列.例如,数列
的一个生成数列.例如,数列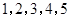 的一个生成数列是
的一个生成数列是 .已知数列
.已知数列 为数列
为数列 的生成数列,
的生成数列, 为数列
为数列 的前
的前 项和.
项和.
(1)写出 的所有可能值;
的所有可能值;
(2)若生成数列 满足的通项公式为
满足的通项公式为 ,求
,求 .
.
给定椭圆 :
: ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 的“准圆”.若椭圆
的“准圆”.若椭圆 的一个焦点为
的一个焦点为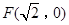 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为 .
.
(1)求椭圆 的方程和其“准圆”方程;
的方程和其“准圆”方程;
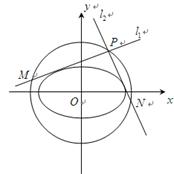
(2)点 是椭圆
是椭圆 的“准圆”上的动点,过点
的“准圆”上的动点,过点 作椭圆的切线
作椭圆的切线 交“准圆”于点
交“准圆”于点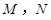 .
.
(ⅰ)当点 为“准圆”与
为“准圆”与 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线 的方程并证明
的方程并证明 ;
;
(ⅱ)求证:线段 的长为定值.
的长为定值.