已知α,β是方程4x2-4tx-1=0(t∈R)的两个实数根,函数f(x)=的定义域为[α,β].
(1)判断f(x)在[α,β]上的单调性,并证明你的结论;
(2)设g(t)=maxf(x)-minf(x),求函数g(t)的最小值
(本小题满分10分)已知单调递增的等比数列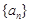 满足:
满足: ,且
,且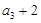 是
是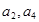 的等差中项.
的等差中项.
(1)求数列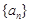 的通项公式;
的通项公式;
(2)若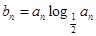 ,
,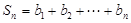 ,求使
,求使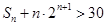 成立的正整数
成立的正整数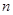 的最小值.
的最小值.
(本小题满分16分)已知数列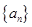 的奇数项是首项为
的奇数项是首项为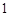 的等差数列,偶数项是首项为
的等差数列,偶数项是首项为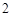 的等比数列,数列
的等比数列,数列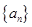 前
前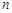 项和为
项和为 ,且满足
,且满足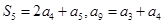 .
.
(1)求数列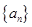 的通项公式;
的通项公式;
(2)若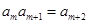 ,求正整数
,求正整数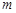 的值;
的值;
(3)是否存在正整数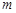 ,使得
,使得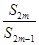 恰好为数列
恰好为数列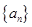 中的一项?若存在,求出所有满足条件的
中的一项?若存在,求出所有满足条件的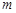 值,若不存在,说明理由.
值,若不存在,说明理由.
(本小题满分16分)设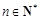 ,函数
,函数
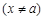 ,其中常数a
,其中常数a .
.
(1)求函数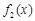 的极值;
的极值;
(2)设一直线与函数 的图象切于两点A(x1,y1),B(x2,y2),且
的图象切于两点A(x1,y1),B(x2,y2),且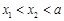 .
.
①求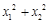 的值;
的值;
②求证: .
.
(本小题满分16分) 如图,过椭圆 的左顶点
的左顶点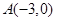 和下顶点
和下顶点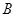 且斜率均为
且斜率均为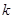 的两直线
的两直线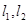 分别交椭圆于
分别交椭圆于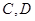 ,又
,又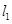 交
交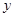 轴于
轴于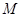 ,
,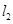 交
交 轴于
轴于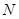 ,且
,且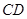 与
与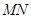 相交于点
相交于点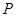 .当
.当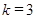 时,
时,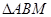 是直角三角形.
是直角三角形.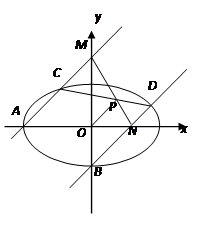
(1)求椭圆L的标准方程;
(2)①证明:存在实数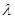 ,使得
,使得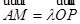 ;
;
②求|OP|的最小值.
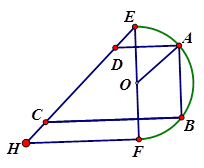
(本小题满分14分)为了制作广告牌,需在如图所示的铁片上切割出一个直角梯形,已知铁片由两部分组成,半径为1的半圆O及等腰直角三角形EFH,其中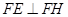 。为裁剪出面积尽可能大的梯形铁片ABCD(不计损耗),将点A,B放在弧EF上,点C、D放在斜边
。为裁剪出面积尽可能大的梯形铁片ABCD(不计损耗),将点A,B放在弧EF上,点C、D放在斜边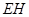 上,且
上,且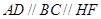 ,设
,设 .
.
(1)求梯形铁片ABCD的面积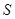 关于
关于 的函数关系式;
的函数关系式;
(2)试确定 的值,使得梯形铁片ABCD的面积
的值,使得梯形铁片ABCD的面积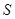 最大,并求出最大值.
最大,并求出最大值.