若函数f(x)对定义域中任意x均满足f(x)+f(2a-x)=2b,则称函数y=f(x)的图象关于点(a,b)对称.
(1)已知函数f(x)=的图象关于点(0,1)对称,求实数m的值;
(2)已知函数g(x)在(-∞,0)∪(0,+∞)上的图象关于点(0,1)对称,且当x∈(0,+∞)时,g(x)=x2+ax+1,求函数g(x)在(-∞,0)上的解析式;
(3)在(1)(2)的条件下,当t>0时,若对任意实数x∈(-∞,0),恒有g(x)<f(t)成立,求实数a的取值范围.
(本试卷共40分,考试时间30分钟)
21.(选做题)本大题包括A,B,C,D共4小题,请从这4题中选做2小题. 每小题10分,共20分.请在答题卡上准确填涂题目标记. 解答时应写出文字说明、证明过程或演算步骤.
A. 选修4-1:几何证明选讲
如图,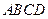 是边长为
是边长为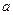 的正方形,以
的正方形,以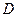 为圆心,
为圆心,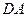 为半径的圆弧与以
为半径的圆弧与以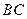 为直径的半⊙O交于点
为直径的半⊙O交于点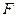 ,延长
,延长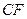 交
交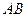 于
于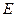 .
.
(1)求证: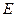 是
是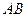 的中点;(2)求线段
的中点;(2)求线段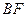 的长.
的长.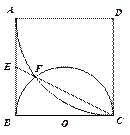
(本小题共16分)
已知数列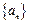 各项均不为0,其前
各项均不为0,其前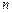 项和为
项和为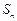 ,且对任意
,且对任意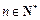 都有
都有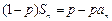 (
(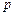 为大于1的常数),记f(n)
为大于1的常数),记f(n)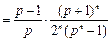 .
.
(1)求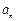 ;
;
(2)试比较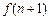 与
与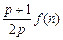 的大小(
的大小(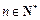 );
);
(3)求证:(2n-1)f(n)≤f(1)+f(2)+…+f(2n-1) ≤[1-()2n-1] (n∈N*)
(本小题共16分)
已知M(p, q)为直线x+y-m=0与曲线y=-的交点,且p<q,若f(x)=,λ、μ为正实数。求证:|f()-f()|<|p-q|
(本小题共16分)
已知椭圆 和圆
和圆 :
: ,过椭圆上一点
,过椭圆上一点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 . (1)①若圆
. (1)①若圆 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率 ; ②若椭圆上存在点
; ②若椭圆上存在点 ,使得
,使得 ,求椭圆离心率
,求椭圆离心率 的取值(2)设直线
的取值(2)设直线 与
与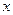 轴、
轴、 轴分别交于点
轴分别交于点 ,
,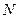 ,求证:
,求证: 为定值.
为定值.
(本小题满分14分)
如图:设工地有一个吊臂长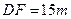 的吊车,吊车底座
的吊车,吊车底座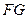 高
高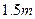 ,现准备把一个底半径为
,现准备把一个底半径为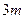 高
高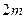 的圆柱形工件吊起平放到
的圆柱形工件吊起平放到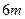 高的桥墩上,问能否将工件吊到桥墩上?(参考数据:
高的桥墩上,问能否将工件吊到桥墩上?(参考数据: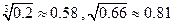 )
)