已知函数f(x)=cos +2sin2x,x∈R.
+2sin2x,x∈R.
(1)求函数f(x)的最小正周期及对称轴方程;
(2)当x∈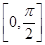 时,求函数f(x)的最大值和最小值及相应的x值.
时,求函数f(x)的最大值和最小值及相应的x值.
将数字1,2,3,4任意排成一列,如果数字k恰好出现在第k个位置上,则称之为一个巧合,求巧合数的数学期望.
证明:事件在一次实验中发生的次数的方差不超过 .
.
一台设备由三大部件组成,在设备运转中,各部件需要调整的概率相应为0.10,0.20和0.30.假设各部件的状态相互独立,以ξ表示同时需要调整的部件数,试求ξ的数学期望Eξ和方差Dξ.
袋中有4只红球,3只黑球,今从袋中随机取出4只球.设取到一只红球得2分,取到一只黑球得1分,试求得分ξ的概率分布和数学期望.
一次单元测试由50个选择题构成,每个选择题有4个选项,其中恰有1个是正确答案.每题选择正确得2分,不选或错选得0分,满分是100分.学生甲选对任一题的概率为0.8,求他在这次测试中成绩的期望和标准差..