某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为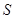 平方米.
平方米.
(1)分别写出用 表示
表示 和用
和用 表示
表示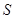 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
【2015高考新课标2,理19】
如图,长方体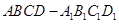 中,
中,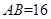 ,
, ,
,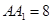 ,点
,点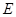 ,
,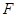 分别在
分别在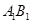 ,
,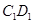 上,
上,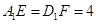 .过点
.过点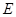 ,
,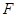 的平面
的平面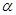 与此长方体的面相交,交线围成一个正方形.
与此长方体的面相交,交线围成一个正方形.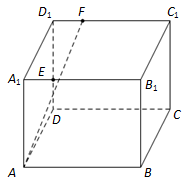
(Ⅰ)在图中画出这个正方形(不必说出画法和理由);
(Ⅱ)求直线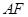 与平面
与平面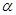 所成角的正弦值.
所成角的正弦值.
【2015高考上海,理21】已知椭圆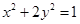 ,过原点的两条直线
,过原点的两条直线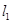 和
和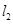 分别于椭圆交于
分别于椭圆交于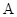 、
、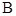 和
和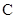 、
、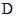 ,记得到的平行四边形
,记得到的平行四边形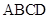 的面积为
的面积为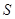 .
.
(1)设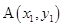 ,
,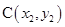 ,用
,用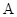 、
、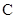 的坐标表示点
的坐标表示点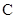 到直线
到直线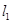 的距离,并证明
的距离,并证明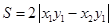 ;
;
(2)设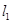 与
与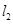 的斜率之积为
的斜率之积为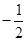 ,求面积
,求面积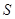 的值.
的值.
【2015高考湖南,理20】已知抛物线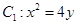 的焦点
的焦点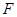 也是椭圆
也是椭圆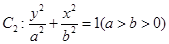 的一个焦点,
的一个焦点,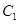 与
与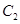 的公共弦的长为
的公共弦的长为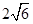 .
.
(1)求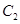 的方程;
的方程;
(2)过点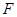 的直线
的直线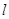 与
与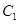 相交于
相交于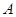 ,
,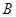 两点,与
两点,与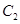 相交于
相交于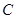 ,
,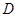 两点,且
两点,且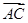 与
与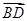 同向
同向
(ⅰ)若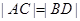 ,求直线
,求直线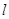 的斜率
的斜率
(ⅱ)设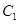 在点
在点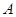 处的切线与
处的切线与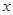 轴的交点为
轴的交点为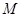 ,证明:直线
,证明:直线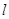 绕点
绕点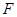 旋转时,
旋转时,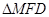 总是钝角三角形
总是钝角三角形
【2015高考北京,理19】已知椭圆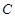 :
: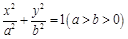 的离心率为
的离心率为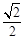 ,点
,点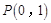 和点
和点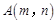
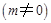 都在椭圆
都在椭圆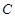 上,直线
上,直线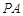 交
交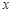 轴于点
轴于点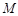 .
.
(Ⅰ)求椭圆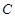 的方程,并求点
的方程,并求点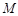 的坐标(用
的坐标(用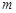 ,
,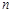 表示);
表示);
(Ⅱ)设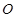 为原点,点
为原点,点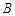 与点
与点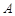 关于
关于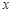 轴对称,直线
轴对称,直线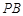 交
交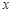 轴于点
轴于点 .问:
.问: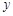 轴上是否存在点
轴上是否存在点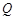 ,使得
,使得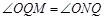 ?若存在,求点
?若存在,求点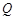 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【2015高考新课标1,理20】在直角坐标系 中,曲线C:y=
中,曲线C:y=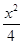 与直线
与直线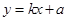 (
(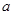 >0)交与M,N两点,
>0)交与M,N两点,
(Ⅰ)当k=0时,分别求C在点M和N处的切线方程;
(Ⅱ)y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.