【2015高考上海,理21】已知椭圆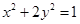 ,过原点的两条直线
,过原点的两条直线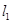 和
和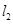 分别于椭圆交于
分别于椭圆交于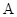 、
、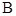 和
和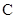 、
、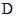 ,记得到的平行四边形
,记得到的平行四边形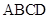 的面积为
的面积为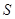 .
.
(1)设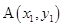 ,
,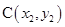 ,用
,用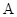 、
、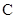 的坐标表示点
的坐标表示点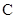 到直线
到直线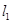 的距离,并证明
的距离,并证明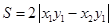 ;
;
(2)设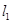 与
与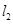 的斜率之积为
的斜率之积为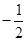 ,求面积
,求面积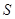 的值.
的值.
如图,三棱柱ABC-A1B1C1中,M,N分别为AB,B1C1的中点.
(1)求证:MN∥平面AA1C1C;
(2)若CC1=CB1,CA=CB,平面CC1B1B⊥平面ABC,求证:AB^平面CMN.
已知函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点( ,-2).
,-2).
(1)求φ的值;
(2)若f( )=
)= ,-
,- <α<0,求sin(2α-
<α<0,求sin(2α- )的值.
)的值.
已知函数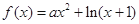 .
.
(1)当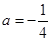 时,求函数
时,求函数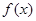 的单调区间;
的单调区间;
(2)当 时,函数
时,函数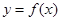 图象上的点都在
图象上的点都在 ,所表示的平面区域内,不等式
,所表示的平面区域内,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度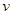 (单位:千米
(单位:千米
/小时)是车流密度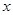 (单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车
(单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车
流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明,当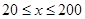 时,
时,
车流速度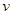 是车流密度
是车流密度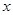 的一次函数.
的一次函数.
(1)当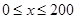 时,求函数
时,求函数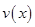 的表达式.
的表达式.
(2)当车流密度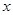 为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)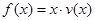 可以达到最大,并求最大值(精确到1辆/每小时).
可以达到最大,并求最大值(精确到1辆/每小时).
在△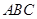 中,内角
中,内角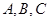 的对边分别为
的对边分别为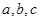 ,已知
,已知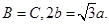
(1)求 的值;
的值;
(2) 的值.
的值.