已知f(x)是定义在[－1,1]上的奇函数，当x∈[－1,0]时的解析式为f(x)＝－(a∈R)．
(1)写出f(x)在(0,1]上的解析式；
(2)求f(x)在(0,1]上的最大值．
已知函数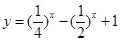
的定义域为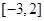
.
（1）求函数的单调区间；（2）求函数的值域.
已知圆C：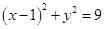
内有一点P（2，2），过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时，求直线l的方程；
(2)当弦AB被点P平分时，写出直线l的方程；
(3) 当直线l的倾斜角为45º时，求弦AB的长.
(12分)设有半径为3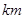
的圆形村落，A、B两人同时从村落中心出发，B向北直行，A先向东直行，出村后不久，改变前进方向，沿着与村落周界相切的直线前进，后来恰与B相遇.设A、B两人速度一定，其速度比为3：1，问两人在何处相遇？
(12分) 已知圆C同时满足下列三个条件：①与y轴相切;②在直线y=x上截得弦长为2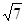
;③圆心在直线x－3y=0上. 求圆C的方程.
如图，在正方体ABCD-A1B1C1D1中，E、F、G分别是CB、CD、CC1的中点，
求证：平面A B1D1∥平面EFG;
（2）求证：平面AA1C⊥面EFG.