已知函数
(1)若函数 在
在 和
和 时取得极值,当
时取得极值,当 时,
时, <2|c|恒成立,求c的取值范围
<2|c|恒成立,求c的取值范围
(2)若 写出使的g(x)>f
写出使的g(x)>f (x)的x取值范围。
(x)的x取值范围。

(本小题14分)
设函数 ,其中
,其中 .
.
(I)当 时,判断函数
时,判断函数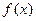 在定义域上的单调性;
在定义域上的单调性;
(II)求函数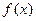 的极值点;
的极值点;
(III)证明对任意的正整数 ,不等式
,不等式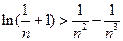 都成立.
都成立.
(本小题13分)
设等比数列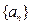 的前项和为
的前项和为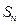 ,首项
,首项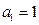 ,公比
,公比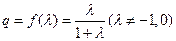 .
.
(I)证明: ;
;
(II)若数列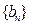 满足
满足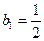 ,
,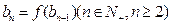 ,求数列
,求数列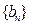 的通项公式;
的通项公式;
(III)记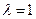 ,
,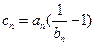 ,数列
,数列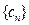 的前项和为
的前项和为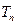 ,求证:当
,求证:当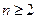 时,
时, .
.
(本小题12分)
为了拓展网络市场,腾讯公司为QQ用户推出了多款QQ应用,如“QQ农场”、“QQ音乐”、“QQ读书”等.市场调查表明,QQ用户在选择以上三种应用时,选择农场、音乐、读书的概率分别为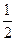 ,
,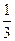 ,
,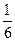 .现有甲、乙、丙三位QQ用户独立任意选择以上三种应用中的一种进行添加.
.现有甲、乙、丙三位QQ用户独立任意选择以上三种应用中的一种进行添加.
(I)求三人所选择的应用互不相同的概率;
(II)记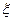 为三人中选择的应用是QQ农场与QQ音乐的人数,求
为三人中选择的应用是QQ农场与QQ音乐的人数,求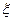 的分布列与数学期望.
的分布列与数学期望.
(本小题12分)
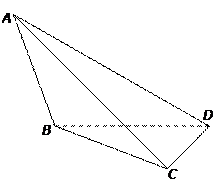
如图,在三棱锥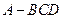 中,侧面
中,侧面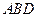 、
、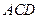 是全等的直角三角形,
是全等的直角三角形, 是公共的斜边,且
是公共的斜边,且 ,
,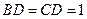 ,另一个侧面是正三角形.
,另一个侧面是正三角形.
(I)求证: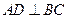 ;
;
(II)求二面角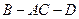 的余弦值;
的余弦值;
(III)在直线 是否存在一点
是否存在一点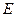 ,使直线
,使直线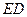 与面
与面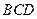 成
成 角?若存在,确定
角?若存在,确定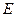 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
(本小题12分)
在某个以旅游业为主的地区,每年各个月份从事旅游服务工作的人数会发生周期性变化.现假设该地区每年各个月份从事旅游服务工作的人数 可近似地用函数
可近似地用函数 来刻画.其中:正整数
来刻画.其中:正整数 表示月份且
表示月份且 ,例如
,例如 时表示1月份;
时表示1月份; 和
和 是正整数;
是正整数; .
.
统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:
①各年相同的月份,该地区从事旅游服务工作的人数基本相同;
②该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差约400人;
③2月份该地区从事旅游服务工作的人数约为100人,随后逐月递增直到8月份达到最多.
(I)试根据已知信息,确定一个符合条件的 的表达式;
的表达式;
(II)一般地,当该地区从事旅游服务工作的人数超过400人时,该地区进入了一年中的旅游“旺季”.那么,一年中的哪几个月是该地区的旅游“旺季”?请说明理由.