(本小题满分16分)
对于函数y=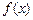 ,x∈(0,
,x∈(0,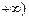 ,如果a,b,c是一个三角形的三边长,那么
,如果a,b,c是一个三角形的三边长,那么 ,
,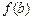 ,
, 也是一个三角形的三边长, 则称函数
也是一个三角形的三边长, 则称函数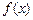 为“保三角形函数”.
为“保三角形函数”.
对于函数y=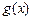 ,x∈
,x∈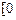 ,
,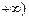 ,如果a,b,c是任意的非负实数,都有
,如果a,b,c是任意的非负实数,都有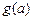 ,
, ,
,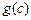 是一个三角形的三边长,则称函数
是一个三角形的三边长,则称函数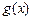 为“恒三角形函数”.
为“恒三角形函数”.
(1)判断三个函数“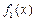 =x,
=x, =
=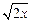 ,
, =
= (定义域均为x∈(0,
(定义域均为x∈(0,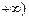 )”中,那些是“保三角形函数”?请说明理由;
)”中,那些是“保三角形函数”?请说明理由;
(2)若函数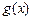 =
= ,x∈
,x∈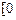 ,
,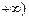 是“恒三角形函数”,试求实数k的取值范围;
是“恒三角形函数”,试求实数k的取值范围;
(3)如果函数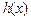 是定义在(0,
是定义在(0,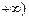 上的周期函数,且值域也为(0,
上的周期函数,且值域也为(0,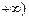 ,试证明:
,试证明: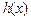 既不是“恒三角形函数”,也不是“保三角形函数”.
既不是“恒三角形函数”,也不是“保三角形函数”.
在平面直角坐标系 中,抛物线C的顶点在原点,经过点
中,抛物线C的顶点在原点,经过点
A(2,2),其焦点F在 轴上.
轴上.
(Ⅰ)求抛物线C的标准方程;
(Ⅱ)求过点F,且与直线OA垂直的直线的方程.
在 中,
中,
(Ⅰ)求AB的值.
(Ⅱ)求 的值.
的值.
设命题 :函数
:函数 =
= -2
-2 -1在区间(-∞,3]上单调递减;命题
-1在区间(-∞,3]上单调递减;命题 :函数
:函数 的定义域是
的定义域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求
为假命题,求 的
的 取值范围.
取值范围.
(本小题14分)
已知 ,函数
,函数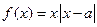 ,
, (Ⅰ)当
(Ⅰ)当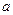 =2时,写出函数
=2时,写出函数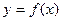 的单调递增区间;
的单调递增区间; (Ⅱ)当
(Ⅱ)当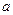 >2时,求函数
>2时,求函数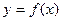 在区间
在区间 上的最小值;
上的最小值; (Ⅲ)设
(Ⅲ)设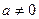 ,函数
,函数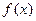 在
在 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出 的取值范围(用
的取值范围(用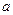 表示)
表示)
(本小题14分)
已知直线L被两平行直线 :
: 与
与 :
: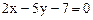 所截线段AB的中点恰在直线
所截线段AB的中点恰在直线 上,已知
上,已知 圆
圆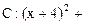
 .
.
(Ⅰ)求两平行直线 与
与 的距离;
的距离;
(Ⅱ)证明直线L与圆C恒有两个交 点;
点; (Ⅲ)求直线L被圆C截得的弦长最小时的方程
(Ⅲ)求直线L被圆C截得的弦长最小时的方程 .
.