如图，AB
为⊙O的直径，AB=4，点C在⊙O上， CF⊥OC，且CF=BF.
（1）证明BF是⊙O的切线;
（2）设AC与BF的延长线交于点M，若MC=6，求∠MCF的大小.
如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处．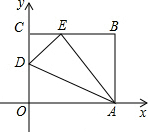
（1）求CE和OD的长；
（2）求直线DE的表达式；
（3）直线y=kx+b与DE平行，当它与矩形OABC有公共点时，直接写出b的取值范围．
某蒜薹（tái）生产基地喜获丰收，收获蒜薹200吨，经市场调查，可采用批发、零售、冷库储藏后销售三种方式，并且按这三种方式销售，计划每吨平均的售价及成本如下表：
| 销售方式 |
批发 |
零售 |
储藏后销售 |
| 售价（百元/吨） |
3 0 |
4 5 |
5 5 |
| 成本（百元/吨） |
7 |
1 0 |
1 2 |
若蒜薹按计划全部售出获得的总利润为y（百元），蒜薹零售x（吨），且批发量是零售量的3倍．
（1）求y与x之间的函数关系式；
（2）由于受条件限制，经冷库储藏售出的蒜薹最多80吨，求该生产基地按计划全部售完蒜薹获得的最大利润．
计算
（1）
－
；
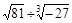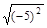（2）
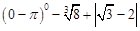
（3）解方程：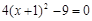
．
已知一次函数y="kx+k+2" ,
（1）若它的图像不经过第三象限，则k的取值范围是 ．
（2）当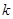
取不同的值时，它的图像一定经过定点______________．（写出定点坐标）
出租车司机老王某天上午营运全是在东西走向的解放路上进行，如果规定向东为正，向西为负，他这天上午行车里程（单位：km）如下：
+8，+4，-10，-3，+6，-5，-2，-7，+4，+6，-9，-11．
（1）将最后一名乘客送到目的地时，老王距上午出发点多远？
（2）若汽车耗油量为0．4L/km，这天上午老王耗油多少升？